Trong mặt phẳng cho 10 điểm A,Az;A:AriAs;AA);AA);A, đôi một không trung nhau. Hỏi thành lập được bao véc tơ có các điểm đầu và điểm cuối là các điểm đó.
H24
Những câu hỏi liên quan
Cho hai đường thẳng xx'/yy'. Lấy điểm A và B lần lượt thuộc đường thẳng xx' và yy'. Trong nửa mặt phẳng bờ xx' chứa đường thẳng yy' kẻ tia Az và trong nửa mặt phẳng bờ yy' chứa đường thẳng xx' kẻ tia Bt sao cho zAx=tBy'. Lấy hai điểm C thuộc Az và D thuộc Bt.
a) Chứng minh rằng ACD=CDB
b) Kẻ các tia phân giác Am của zAx và tia phân giác Bn của tBy'. Chứng minh rằng Am//Bn
Cho hai đường thẳng xx/yy. Lấy điểm A và B lần lượt thuộc đường thẳng xx và yy. Trong nửa mặt phẳng bờ xx chứa đường thẳng yy kẻ tia Az và trong nửa mặt phẳng bờ yy chứa đường thẳng xx kẻ tia Bt sao cho zAxtBy. Lấy hai điểm C thuộc Az và D thuộc Bt.a) Chứng minh rằng ACDCDBb) Kẻ các tia phân giác Am của zAx và tia phân giác Bn của tBy. Chứng minh rằng Am//BnMk đg cần gấp. TKS mn
Đọc tiếp
Cho hai đường thẳng xx'/yy'. Lấy điểm A và B lần lượt thuộc đường thẳng xx' và yy'. Trong nửa mặt phẳng bờ xx' chứa đường thẳng yy' kẻ tia Az và trong nửa mặt phẳng bờ yy' chứa đường thẳng xx' kẻ tia Bt sao cho zAx=tBy'. Lấy hai điểm C thuộc Az và D thuộc Bt.
a) Chứng minh rằng ACD=CDB
b) Kẻ các tia phân giác Am của zAx và tia phân giác Bn của tBy'. Chứng minh rằng Am//Bn
Mk đg cần gấp. TKS mn
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y - 2z + 1 0, (Q): 2x + 4y + az + b 0. Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1. A. a-4 và b8 B. a-4 và b8 hoặc b-4 C. a-2 và b38 hoặc b-34 D. a-4 và b38 hoặc b-34
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y - 2z + 1 = 0, (Q): 2x + 4y + az + b = 0. Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1.
A. a=-4 và b=8
B. a=-4 và b=8 hoặc b=-4
C. a=-2 và b=38 hoặc b=-34
D. a=-4 và b=38 hoặc b=-34
Đáp án B
Muốn khoảng cách giữa hai mặt phẳng (P) và (Q) lớn hơn 0 thì trước hết hai mặt phẳng đó phải song song (nếu hai mặt phẳng đó trùng nhau hoặc cắt nhau thì khoảng cách giữa chúng sẽ bằng 0). Do đó ta có:
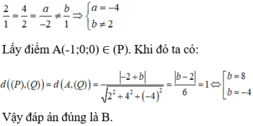
Đúng 0
Bình luận (0)
Cho góc xOy = 1400. . Trên tia Ox lấy điểm A, qua A vẽ tia Az sao cho tia Az và tia Oy nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox và góc OAz = 400.
a)Chứng minh Az // Oy
b)Vẽ tia At là tia đối của của tia Az. Chứng minh hai đường phân giác của hai góc xOy và OAt song song với nhau.
a, Vì \(\widehat{xOy}+\widehat{OAz}=140^0+40^0=180^0\) mà 2 góc này ở vị trí TCP nên Az//Oy
b, Gọi Om,On lần lượt là p/g \(\widehat{xOy};\widehat{OAt}\)
Ta có \(\widehat{OAt}=180^0-\widehat{OAz}=140^0\left(kề.bù\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{mOx}=\dfrac{1}{2}\widehat{xOy}=70^0\\\widehat{nAO}=\dfrac{1}{2}\widehat{OAt}=70^0\end{matrix}\right.\Rightarrow\widehat{mOx}=\widehat{nAO}\) mà 2 góc này ở vị trí SLT nên Om//On
Do đó 2 đg p/g của \(\widehat{xOy}\) và \(\widehat{OAt}\) song song vs nhau
Đúng 2
Bình luận (0)
Bài 7.Cho góc xOy = 140 độ. Trên tia Ox lấy điểm A, qua A vẽ tia Az sao cho tia Az và tia Oy nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox và góc OAz = 40 độ.
a)Chứng minh Az // Oy
b)Vẽ tia At là tia đối của của tia Az. Chứng minh hai đường phân giác của hai góc xOy và OAt song song với nhau.
a, Vì \(\widehat{OAz}+\widehat{xOy}=140^0+40^0=180^0\) mà 2 góc này ở vị trí tcp nên Az//Oy
b, Vì At đối Az nên \(\widehat{OAt}=180^0-\widehat{OAz}=140^0\left(kề.bù\right)\)
Gọi Om là p/g \(\widehat{xOy}\), On là p/g \(\widehat{OAt}\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{mOx}=\dfrac{1}{2}\widehat{xOy}=70^0\\\widehat{OAn}=\dfrac{1}{2}\widehat{OAt}=70^0\end{matrix}\right.\\ \Rightarrow\widehat{mOx}=\widehat{OAn}\)
Do đó ta đc dpcm
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm M(0;1;3), N(10;6;0) và mặt phẳng (P): x - 2y + 2z -10 0. Điểm I(-10; a; b) thuộc mặt phẳng (P) sao cho |IM - IN| lớn nhất. Khi đó tổng T a + b bằng: A. T 5 B. T 1 C. T 2 D. T 6
Đọc tiếp
Trong không gian Oxyz, cho hai điểm M(0;1;3), N(10;6;0) và mặt phẳng (P): x - 2y + 2z -10 = 0. Điểm I(-10; a; b) thuộc mặt phẳng (P) sao cho |IM - IN| lớn nhất. Khi đó tổng T = a + b bằng:
A. T = 5
B. T = 1
C. T = 2
D. T = 6
Chọn C
Ta có:
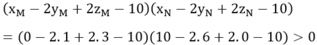
Nên hai điểm M và N nằm cùng phía so với mặt phẳng (P)
Ta luôn có: ![]() , nên |IM - IN| lớn nhất khi và chỉ khi I là giao điểm của đường thẳng MN với mặt phẳng (P).
, nên |IM - IN| lớn nhất khi và chỉ khi I là giao điểm của đường thẳng MN với mặt phẳng (P).
Đường thẳng MN có vec-tơ chỉ phương ![]() , nên phương trình đường thẳng MN là:
, nên phương trình đường thẳng MN là: 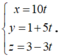
Tọa độ giao điểm I của đường thẳng MN với mặt phẳng (P) ứng với t là nghiệm phương trình:
10t - 2(1+5t) + 2(3-3t) - 10 = 0 <=> t = -1
Do đó I (-10; -4; 6), từ đó ta có a = -4 và b = 6, nên T = -4 + 6 = 2.
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm Y đường kính AB bán kính r .Từ A và B vẽ các tiếp tuyến AZ,BY trong cùng một nửa mặt phẳng có B là AB với nửa đường tròn tâm Y .Trên nửa đường tròn lấy điểm C ,tiếp tuyến với tâm Y tại C cắt AZ,BY lần lượt tại K và M .Chứng minh a)Ak+BM=KM b)Ak×BM=ABbình chia 4
Trong không gian Oxyz, cho điểm A(-1;3;-2) và mặt phẳng
Q
:
x
−
2
y
−
2
z
−
10
0
. Gọi (P) là mặt phẳng qua A và song song với mặt phẳng (Q). Phương trình của (P) là: A.
x
−
3
y
+
2...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(-1;3;-2) và mặt phẳng Q : x − 2 y − 2 z − 10 = 0 . Gọi (P) là mặt phẳng qua A và song song với mặt phẳng (Q). Phương trình của (P) là:
A. x − 3 y + 2 z − 4 = 0
B. x − 2 y + 2 z + 5 = 0
C. − x + 2 y − 2 z + 3 = 0
D. x − 2 y − 2 z + 3 = 0
Đáp án D
Ta có n ( Q ) → = 1 ; − 2 ; − 2
Vì (P) song song với (Q) nên (P) nhận n ( Q ) → = 1 ; − 2 ; − 2 làm vectơ pháp tuyến.
Mặt phẳng (P) đi qua A(-1;3;-2) và nhận n ( Q ) → = 1 ; − 2 ; − 2 làm vectơ pháp tuyến có phương trình là:
1 x + 1 − 2 y − 3 − 2 z + 2 = 0 ⇔ x − 2 y − 2 z + 3 = 0
Đúng 0
Bình luận (0)
Bài 4: Cho đường thẳng xy, lấy điểm A trên đường thẳng xy. Vẽ tia Az sao cho zAx 120 độ. Trên nửa mặt phẳng bờ xy không chứa tia Az, vẽ tia At sao cho yAt 30 độ.a) Tính số đo các góc yAz; xAt b) Vẽ tia Am trong nửa mặt phẳng bờ xy chứa tia At sao cho yAm 60 độ. Hãy chứng tỏ tia At là tia phân giác của góc yAm.c) Vẽ tia An là tia phân giác của góc xAz. Hỏi tia Az có là tia phân giác của góc yAn không ? Vì sao ?CÁC BẠN GIẢI NHANH VÀ ĐẦY ĐỦ GIÚP MÌNH NHA!!!
Đọc tiếp
Bài 4: Cho đường thẳng xy, lấy điểm A trên đường thẳng xy. Vẽ tia Az sao cho zAx =120 độ. Trên nửa mặt phẳng bờ xy không chứa tia Az, vẽ tia At sao cho yAt = 30 độ.
a) Tính số đo các góc yAz; xAt
b) Vẽ tia Am trong nửa mặt phẳng bờ xy chứa tia At sao cho yAm = 60 độ. Hãy chứng tỏ tia At là tia phân giác của góc yAm.
c) Vẽ tia An là tia phân giác của góc xAz. Hỏi tia Az có là tia phân giác của góc yAn không ? Vì sao ?
CÁC BẠN GIẢI NHANH VÀ ĐẦY ĐỦ GIÚP MÌNH NHA!!!


