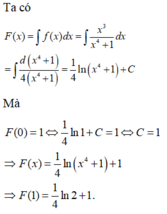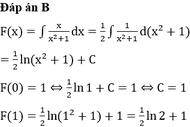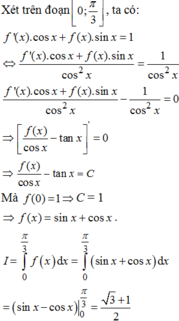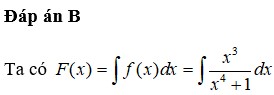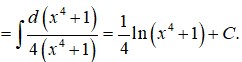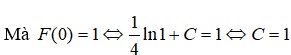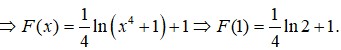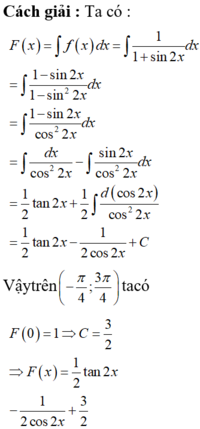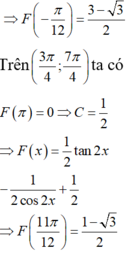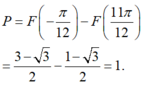Cho f’(x) =f’(x-1) . Biết f(0)=1 ,f(1)=2019. Tính nguyên hàm tích phân từ [0,1] của f(x)
KD
Những câu hỏi liên quan
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) 0, F(2) 1, G(2) 1 và
∫
0
2
F
(
x
)
g
(
x
)
d
x
3 . Tính tích phân hàm:
∫
0
2
G
(
x
)
f
(
x
)
d
x
A. I 3. B. I 0....
Đọc tiếp
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Đúng 0
Bình luận (0)
cho hàm số f(x)=ax2+bx+c ( x là ẩn , a,b,c là hệ số ) . Biết rằng f(0)=2018, f(1)=2019,f(-1)=2017 . Tính f(-2019)
Cho f(x)
x
x
2
+
1
(
2
x
2
+
1
+
2017
)
, biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)2018. Tính F(2) A. F(2) 5+2017
5
B. F(2) 4+2017
4
C. F(2) 3+2017
3...
Đọc tiếp
Cho f(x)= x x 2 + 1 ( 2 x 2 + 1 + 2017 ) , biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)=2018. Tính F(2)
A. F(2) = 5+2017 5
B. F(2) = 4+2017 4
C. F(2) = 3+2017 3
D. F(2)= 2022
Biết F(x) là một nguyên hàm của hàm số
f
(
x
)
x
3
x
4
+
1
và F(0) 1. Tính F(1)
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f ( x ) = x 3 x 4 + 1 và F(0) = 1. Tính F(1)
![]()
![]()
![]()
Biết F(x) là một nguyên hàm của hàm số f ( x ) = x x 2 + 1 và F(0) = 1.Tính F(1).
A. F(1) = ln2 + 1
B. F(1) = 1 2 ln2 + 1
C. F(1) = 0
D. F(1) = ln2 + 2
Cho hàm số yf(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx1, x ϵ [0;π/3] và f(0)1. Tính tích phân
I
∫
0
π
3
f
x
d
x
A. 1/2 + π/3 B.
3
+
1
2
C. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Biết F(x) là một nguyên hàm của hàm số
f
(
x
)
x
3
x
4
+
1
và F(0)1. Tính F(1) A.
F
(
1
)
ln
2
+
1
B.
F
(
1
)
1
4
ln
2...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f ( x ) = x 3 x 4 + 1 và F(0)=1. Tính F(1)
A. F ( 1 ) = ln 2 + 1
B. F ( 1 ) = 1 4 ln 2 + 1
C. F ( 1 ) = ln 2 - 1
D. F ( 1 ) = 1 4 ln 2 - 1
Cho hàm số f(x)= x +1/4 Tính tổng f(0)+f(1/2021)+f(2/2021)+f(3/2021)+...+f(2019/2021)+f(2020/2021)+f(1)
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
1
+
sin
2
x
với
x
∈
R
{
-
π
4
+
k
π
,
k
∈
}...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 1 + sin 2 x với x ∈ R { - π 4 + k π , k ∈ } . Biết F(0)=1,F( π )=0, tính giá trị biểu thức P = F ( - π 12 ) - F ( 11 π 12 )
![]()
![]()
![]()
![]()