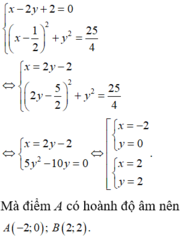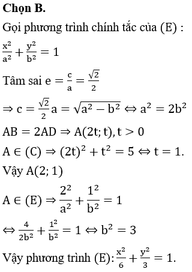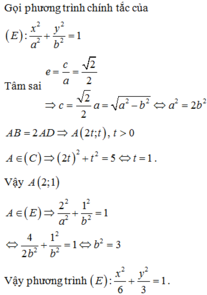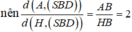trong mặt phẳng Õy, cho hình chữ nhật ABCD có AB=2AD, hai điểm M(1;1);N(2;0) lần lượt nằm trên hai đường thẳng chứa cạnh AB,AD. xác định của hình chữ nhật ABCD biết ABCD có tâm là gốc tọa độ và xA<1
IH
Những câu hỏi liên quan
Trong mặt phẳng toạ độ Oxy cho hình chữ nhật ABCD tâm I có AB = 2AD . Gọi M là trung điểm AB và N là điểm thuộc đoạn AC sao NC = 4IN . Giả sử M(2;5), N(1;7). Viết phương trình đường thẳng CD.
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm
I
1
2
;
0
phương trình đường thẳng AB là x-2y+20 và AB2AD Tìm tọa độ điểm B, biết rằng điểm A có hoành độ âm A. B(-2;0) B. (2;2) C. B(3;0) D. (-1;-2)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm I 1 2 ; 0 phương trình đường thẳng AB là x-2y+2=0 và AB=2AD Tìm tọa độ điểm B, biết rằng điểm A có hoành độ âm
A. B(-2;0)
B. (2;2)
C. B(3;0)
D. (-1;-2)
Trong mặt phẳng Oxy, cho elip (E) có tâm sai e bằng 22 và cắt đường tròn (C) có phương trình tại bốn điểm tạo thành hình chữ nhật ABCD có AB2AD. Phương trình chính tắc của (E) là A.
x
2
12
+
y
2
3
1
B.
x
2...
Đọc tiếp
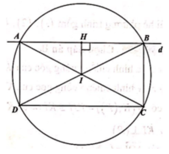
Trong mặt phẳng Oxy, cho elip (E) có tâm sai e bằng 22 và cắt đường tròn (C) có phương trình tại bốn điểm tạo thành hình chữ nhật ABCD có AB=2AD. Phương trình chính tắc của (E) là
A. x 2 12 + y 2 3 = 1
B. x 2 6 + y 2 3 = 1
C. x 2 9 + y 2 9 2 = 1
D. x 2 8 + y 2 4 = 1
Trong mặt phẳng Oxy, cho elip (E) có tâm sai e bằng
2
2
và cắt đường tròn (C) có phương trình
x
2
+
y
2
5
tại bốn điểm tạo thành hình chữ nhật ABCD có AB2AD. Phương trình chính tắc của (E) là
Đọc tiếp
Trong mặt phẳng Oxy, cho elip (E) có tâm sai e bằng 2 2 và cắt đường tròn (C) có phương trình x 2 + y 2 = 5 tại bốn điểm tạo thành hình chữ nhật ABCD có AB=2AD. Phương trình chính tắc của (E) là
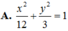
![]()
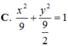
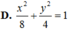
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA AB 2AD 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính mặt cầu tâm B cắt SC theo một dây có độ dài 2a là: A.
2
a
2
3
B.
2
a
11
3
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính mặt cầu tâm B cắt SC theo một dây có độ dài 2a là:
A. 2 a 2 3
B. 2 a 11 3
C. a 17 3
D. a 10
Đáp án C
Do (SAB) ⊥ (ABCD) và (SAD) ⊥ (ABCD) ta có SA ⊥ (ABCD). Theo định lí ba đường vuông góc ta có BC ⊥ SB.
Hạ BH ⊥ SC tại H. Xét tam giác vuông SBC ta có:
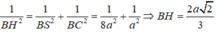
Ta có mặt cầu S(B;r) cắt đường thẳng SC theo một dây cung có độ dài 2a khi và chỉ khi ta có
![]()
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB 2AD 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ điểm A đến mặt phẳng (SBD). A.
a
3
4
B.
a
3
2
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2AD = 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ điểm A đến mặt phẳng (SBD).
A. a 3 4
B. a 3 2
C. a 2
D. a
Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB 2AD 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ điểm A đến mặt phẳng (SBD). A.
a
3
4
B.
a
3
2
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2AD = 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ điểm A đến mặt phẳng (SBD).
A. a 3 4
B. a 3 2
C. a 2
D. a
Đáp án là B
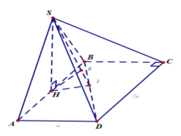
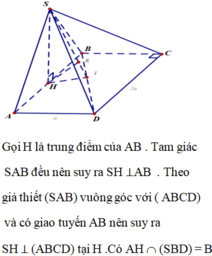
Gọi H là trung điểm của AB . Tam giác SAB đều nên suy ra SH ⊥AB . Theo giả thiết (SAB) vuông góc với ( ABCD) và có giao tuyến AB nên suy ra SH ⊥ (ABCD) tại H . Có AH ∩ (SBD) = B nên
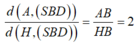
![]()
Trong ( ABCD) kẻ HI ⊥ BD tại I , kết hợp SH ⊥ (ABCD) ta suy ra
BD⊥ (SHI) => (SHI) ⊥ (SBD) , mà (SHI ) ∩ (SBD) = SI nên trong (SHI) nếu ta kẻ HK ⊥ SI tại K thì HK ⊥ (SBD) tại K , do đó HK = d (H,( SBD)) .
Ta tính được :
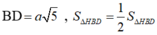
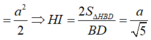
Tam giác SAB đều cạnh 2a nên SH=a 3
Tam giác SHI vuông tại H đường cao HK nên
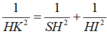
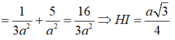
Vậy khoảng cách từ A đến (SBD) là: a 3 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA AB 2AD 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính của mặt cầu ngoại tâm B cắt SC theo một dây có độ dài 2a/3 là: A.
2
a
3
3
B.
2
a
2
3
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính của mặt cầu ngoại tâm B cắt SC theo một dây có độ dài 2a/3 là:
A. 2 a 3 3
B. 2 a 2 3
C. a
D. a 2
Đáp án C
Từ giả thiết ta có SA ⊥ (ABCD), theo định lí ba đường vuông góc ta có tam giác SBC vuông tại B. Gọi S(B,r) là mặt cầu tâm B cắt SC theo một dây có độ dài 2a/3. Khi đó ta tính được:
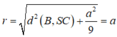
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với mặt phẳng (ABCD),
SA
AB
a
,
AD
3
a
.
Gọi M là trung điểm BC. Tính cos góc tạo bởi hai mặt phẳng (ABCD) và (SDM).
A
.
6...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với mặt phẳng (ABCD), SA = AB = a , AD = 3 a . Gọi M là trung điểm BC. Tính cos góc tạo bởi hai mặt phẳng (ABCD) và (SDM).
A . 6 7 .
B . 5 7 .
C . 3 7 .
D . 1 7 .
Chọn A.
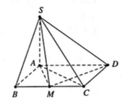
Gắn tọa độ Oxyz, với A(0;0;0), B(1;0;0), D(0;3;0), S(0;0;1)
Khi đó C ( 1 ; 3 ; 0 ) ⇒ Trung điểm M của BC là M ( 1 ; 3 2 ; 0 ) .
Ta có
SM → = ( 1 ; 3 2 ; - 1 ) , SD → = ( 0 ; 3 ; - 1 ) ⇒ [ SM → ; SD → ] = ( 3 2 ; 1 ; 3 ) .
Suy ra n ⃗ ( SDM ) = ( 3 2 ; 1 ; 3 ) mà n ⃗ ( ABCD ) = n ⃗ ( Oxy ) = ( 0 ; 0 ; 1 ) ,
ta được
cos ( SDM ^ ) ; ( ABCD ) = n → ( SDM ) . n → ( ABCD ) n → ( SDM ) . n → ( ABCD ) = 6 7 .
Đúng 0
Bình luận (0)