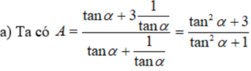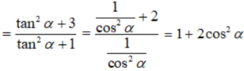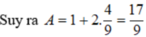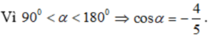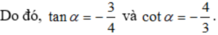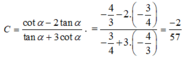Tính giá trị biểu thức A = 102 - (52.4 - 43.3) + 23
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NV
Những câu hỏi liên quan
Tính giá trị biểu thức A tại x -2; y 102; z 102
A
4
x
2
y
3
z
+
2
x
3
y
2
z
2
-
x
2
y
2...
Đọc tiếp
Tính giá trị biểu thức A tại x = -2; y = 102; z = 102
A = 4 x 2 y 3 z + 2 x 3 y 2 z 2 - x 2 y 2 : x 2 y 2
A. 1029
B. -1028
C. 30
D. -1
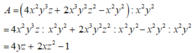
Giá trị biểu thức tại x = -2; y = 102; z= 102 là:
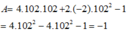
Chọn đáp án D
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức
A
35
2
-
700
+
10
2
. A.
25
2
. B.
15
2
. C.
45
2
. D.
20
2
.
Đọc tiếp
Tính giá trị của biểu thức A = 35 2 - 700 + 10 2 .
A. 25 2 .
B. 15 2 .
C. 45 2 .
D. 20 2 .
Tính giá trị biểu thức A = 2 + 5 + 8 ...+ 102
Đề thấy sai sai. Vì 102 - 2 = 100 không chia hết cho 3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Viết tiếp vào chỗ chấm cho thích hợp :Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính ....... trước.b) Tính :3 x (17 + 22) ...... ......Giá trị của biểu thức 3 x (17 + 22) là ......(58 – 23) : 5 ........ ......Giá trị của biểu thức (58 – 23) : 5 là ........
Đọc tiếp
a) Viết tiếp vào chỗ chấm cho thích hợp :
Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính ....... trước.
b) Tính :
3 x (17 + 22) = ...... = ......
Giá trị của biểu thức 3 x (17 + 22) là ......
(58 – 23) : 5 = ........ = ......
Giá trị của biểu thức (58 – 23) : 5 là ........
a) Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính trong ngoặc trước.
b) Tính :
3 x (17 + 22) = 3 x 39 = 117
Giá trị của biểu thức 3 x (17 + 22) là 117.
(58 – 23) : 5 = 35 : 5 = 7.
Giá trị của biểu thức (58 – 23) : 5 = 7.
Đúng 0
Bình luận (0)
Với a = 8 thì giá trị của biểu thức 127 + 8 x 6 = 127 + 48 = 175
Đúng 0
Bình luận (0)
a) Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính trong ngoặc trước.
b) Tính :
3 x (17 + 22) = 3 x 39
= 117
Giá trị của biểu thức 3 x (17 + 22) là : 117
(58 – 23) : 5 = 35 : 5
= 7
Giá trị của biểu thức (58 – 23) : 5 là 7
Chúc lm bài tốt
Tính giá trị biểu thức
A
28
+
46
+
(
|
−
34
|
+
|
−
40
|
)
B
−
27
+
−
208
+
−
43
+...
Đọc tiếp
Tính giá trị biểu thức
A = 28 + 46 + ( | − 34 | + | − 40 | ) B = − 27 + − 208 + − 43 + − 102
a) Cho
cos
α
2
3
. Tính giá trị của biểu thức
A
tan
α
+
3
c
o
t
α
tan
α
+
c
o
t
α
b) Cho
sin
α
3
5...
Đọc tiếp
a) Cho cos α = 2 3 . Tính giá trị của biểu thức
A = tan α + 3 c o t α tan α + c o t α
b) Cho sin α = 3 5 v à 90 ° < α < 180 °
Tính giá trị của biểu thức:
C = c o t α - 2 tan α tan α + 3 c o t α
Tính giá trị biểu thức :
a) 3499 + 1104 : 23 – 100
b) 4 5 + 2 3 × 1 6
a) 3499 + 1104 : 23 − 100 = 3499 + 48 − 100 = 3447
b) 4 5 + 2 3 × 1 6 = 4 5 + 1 9 = 41 45
Đúng 0
Bình luận (0)
Bài 4: Tính giá trị của biểu thức A = 352 - 700 + 102.
A. 252. B. 152.
C. 452. D. 202.
Bài 4: Tính giá trị của biểu thức A = 352 - 700 + 102.
A. 252. B. 152.
C. 452. D. 202.
Xem thêm câu trả lời
cho các số thực dương a và b tm \(a^{100}+b^{100}=a^{101}+b^{101}=a^{102}+b^{102}\) tính giá trị của biểu thức \(P=a^{2014}+b^{2015}\)
Ta có đẳng thức: \(a^{102}+b^{102}=\left(a^{101}+b^{101}\right)\left(a+b\right)-ab\left(a^{100}+b^{100}\right)\) với mọi số a,b
Kết hợp với: \(a^{100}+b^{100}=a^{101}+b^{101}=a^{102}+b^{102}\)
\(\Rightarrow1=\left(a+b\right)-ab\Leftrightarrow\left(a-1\right)\left(b-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\Rightarrow1+b^{100}=1+b^{101}=1+b^{102}\Rightarrow b=1\\b=1\Rightarrow1+a^{100}=1+a^{101}=1+a^{102}\Rightarrow a=1\end{matrix}\right.\)
Do đó: \(P=a^{2014}+b^{2014}=1^{2004}+1^{2005}=2\)
Đúng 5
Bình luận (0)