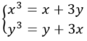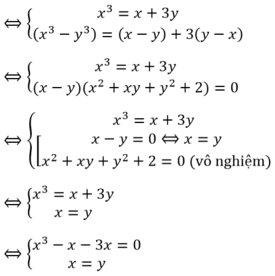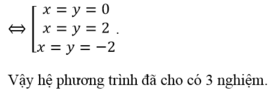giải hệ phương trình x3 -3x = y3 -3y và x6 + y6 =1
KT
Những câu hỏi liên quan
Số nghiệm của hệ phương trình
x
3
-
3
y
y
3
-
3
x
x
6...
Đọc tiếp
Số nghiệm của hệ phương trình x 3 - 3 y = y 3 - 3 x x 6 + y 6 = 27 là:
A. 1
B. 2
C. 6
D. 3
Đáp án: B



Vậy hệ phương trình có 2 nghiệm.
Đúng 0
Bình luận (0)
Hệ phương trình
x
3
−
3
x
y
3
−
3
y
x
6
+...
Đọc tiếp
Hệ phương trình x 3 − 3 x = y 3 − 3 y x 6 + y 6 = 27 có bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 4
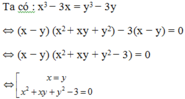
Khi x = y thì x 6 + x 6 = 27 ⇔ x 6 = 27 2 ⇔ x = ± 27 2 6
Do đó hệ có nghiệm ± 27 2 6 ; ± 27 2 6
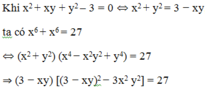
⇔ 3 x y 3 + 27 x y = 0 ⇔ x y = 0 x y 2 = − 9 v ô l ý
Vậy hệ phương trình đã cho có 2 nghiệm.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Số nghiệm của hệ phương trình
x
3
x
+
3
y
y
3...
Đọc tiếp
Số nghiệm của hệ phương trình x 3 = x + 3 y y 3 = y + 3 x là:
A. 2
B. 3
C. 1
D. 4
Giá trị của đa thức tại xy - x2 y2 + x3 y3 - x4 y4 + x5 y5 - x6 y6 tại x -1; y 1 là:(A) 0;(B) -1;(C) 1;(D) -6Hãy chọn phương án đúng.
Đọc tiếp
Giá trị của đa thức tại xy - x2 y2 + x3 y3 - x4 y4 + x5 y5 - x6 y6 tại x = -1; y = 1 là:
(A) 0;
(B) -1;
(C) 1;
(D) -6
Hãy chọn phương án đúng.
Khi x = - 1; y = 1 thì xy = (-1).1= -1
Ta có: xy – x2y2 + x3y3 – x4y4 + x5y5 – x6.y6
= xy – (xy)2 + (xy)3 – (xy)4 + (xy)5 – (xy)6
= -1 – (-1)2 + (-1)3 – (-1)4 + (-1)5 - (-1)6
= -1 – 1 + (-1) – 1 + (-1) – 1
= - 6
Chọn đáp án D
Đúng 0
Bình luận (0)
Cho xyz = 1 và x+y+z = 1/x+1/y+1/z = 0
Tính giá trị M = (x6+y6+z6)/(x3+y3+z3)
Phân tích các đa thức sau thành nhân tử:a) 3x - 3y +
x
2
-
y
2
; b)
x
2
-4
x
2
y
2
+
y
2
+ 2xy c)
x
6
-
x...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) 3x - 3y + x 2 - y 2 ; b) x 2 -4 x 2 y 2 + y 2 + 2xy
c) x 6 - x 4 + 2 x 3 + 2 x 2 ; d) x 3 - 3x 2 +3x - 1 - y 3 .
a) (x - y)(x + y + 3). b) (x + y - 2xy)(2 + y + 2xy).
c) x 2 (x + l)( x 3 - x 2 + 2). d) (x – 1 - y)[ ( x - 1 ) 2 + ( x - 1 ) y + y 2 ].
Đúng 0
Bình luận (0)
Giải hệ phương trình
x
3
+
4
y
y
3
+
16
x
1
+
y...
Đọc tiếp
Giải hệ phương trình x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 )
x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 ) ( 1 )
– Xét x = 0, hệ (I) trở thành 4 y = y 3 y 2 = 4 < = > y = ± 2
– Xét x ≠ 0, đặt y x = t < = > y = x t . Hệ (I) trở thành
x 3 + 4 x t = x 3 t 3 + 16 x 1 + x 2 t 2 = 5 ( 1 + x 2 ) < = > x 3 ( t 3 − 1 ) = 4 x t − 16 x x 2 ( t 2 − 5 ) = 4 < = > x 3 ( t 3 − 1 ) = 4 x ( t − 4 ) ( 1 ) 4 = x 2 ( t 2 − 5 ) ( 2 )
Nhân từng vế của (1) và (2), ta được phương trình hệ quả
4 x 3 ( t 3 − 1 ) = 4 x 3 ( t − 4 ) ( t 2 − 5 ) < = > t 3 − 1 = t 3 − 4 t 2 − 5 t + 20 (Do x ≠ 0) <=>4t 2 + 5 t − 21 = 0 < = > t = − 3 t = 7 4
+ Với t = – 3, thay vào (2) được x2 = 1 ⇔ x = ±1.
x = 1 thì y = –3, thử lại (1;–3) là một nghiệm của (I)
x = –1 thì y = 3, thử lại (–1;3) là một nghiệm của (I)
+ Với t = 7/4 , thay vào (2) được x 2 = − 64 31 (loại)
Vậy hệ (I) có các nghiệm (0;2), (0;–2), (1;–3), (–1;3).
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
1
−
2
x
2
3
x
x
−
3
+
x
−
1
2
;
b)
1
+
x...
Đọc tiếp
Giải các phương trình sau:
a) 1 − 2 x 2 = 3 x x − 3 + x − 1 2 ;
b) 1 + x 3 + 1 − x 3 = 6 x + 1 2 ;
c) x − 4 4 − x + 3 = x 3 − 2 − x 6 ;
d) 5 x + 3 x − 4 5 15 = 3 − x 15 + 7 x 5 + 1 − x .
a) x = 0 b) x = - 1 3
c) x = 28 15 d) x = -82.
Đúng 0
Bình luận (0)
phan tich thanh nhan tu
a) x2+4y2+4xy
b) (x+y)2-(x-y)2
c) (3x+1)2-(x+1)2
d) x6-y6
e) x3+y3+z3-3xyz
xin may ban giup cho m
a) \(x^2+4y^2+4xy\)
\(=x^2+2.x.2y+\left(2y\right)^2\)
\(=\left(x+2y\right)^2\)
b) \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)\left(x+y+x-y\right)\)
\(=2y.2x\)
\(=4xy\)
c) \(\left(3x+1\right)^2-\left(x+1\right)^2\)
\(=\left(3x+1-x-1\right)\left(3x+1+x-1\right)\)
a) \(x^6-y^6=\left(x^2\right)^3-\left(y^2\right)^3\)
\(=\left(x^2-y^2\right)\left(x^4+x^2y^2+y^4\right)\)
Đúng 0
Bình luận (0)
Hệ phương trình
x
3
3
x
+
8
y
y
3
3
y
+
8...
Đọc tiếp
Hệ phương trình x 3 = 3 x + 8 y y 3 = 3 y + 8 x có nghiệm là (x; y) với x ≠ 0 và y ≠ 0 là:
A. − 11 ; − 11 ; 11 ; 11
B. 0 ; 11 ; 11 ; 0
C. − 11 , 0
D. 11 , 0
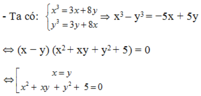
Khi x = y thì x 3 = 11 x = 0 ⇔ x = 0 ; x = ± 11
Khi x 2 + x y + y 2 + 5 = 0 ⇔ x + 1 2 y 2 + 3 4 y 2 + 5 = 0 (phương trình vô nghiệm)
Vậy hệ có nghiệm − 11 ; − 11 ; 11 ; 11
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)