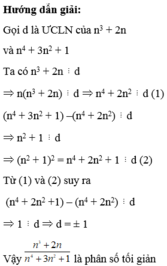Chứng minh với mọi n\(\in\)N* thì n3+n+2 là hợp số
NH
Những câu hỏi liên quan
Chứng minh rằng với mọi số nguyên n thì phân số n 3 + 2 n n 4 + 3 n 2 + 1 là phân số tối giản
Cho A = n6 + 10n4 + n3 + 98n – 6n5 – 26 và B = 1 + n3 – n. Chứng minh với mọi n nguyên thì thương của phép chia A cho B là bội số của 6.
Thực hiện phép chia, ta được:Thương của A chia cho B là n3 – 6n2 + 11n – 6Ta có: 3 2 3 226 11 6 12 6 6( 1) .( 1) 6.(2 1)n n n n n n nn n n n n− + − = − + − −= − + + − −Vì (n-1).n.(n+1) là tích của 3 số nguyên liên tiếp nên tích đó vừa chia hết cho 2, vừa chia hết cho 3 suy ra tích đó chia hết cho 6Mặt khác 6(2n-n2-1) chia hết cho 6=> Th¬ng cña phÐp chia A cho B lµ béi sè cña 6
Xem nội dung đầy đủ tại:https://123doc.org//document/4209455-de-da-hsg-toan-8-huyen-tam-duong-2016-2017.htm
Đúng 0
Bình luận (0)
Chứng minh:a)
50
n
+
2
–
50
n
+
1
chia hết cho 245 với mọi số tự nhiên n.b)
n
3
- n chia hết cho 6 với mọi số nguyên n.
Đọc tiếp
Chứng minh:
a) 50 n + 2 – 50 n + 1 chia hết cho 245 với mọi số tự nhiên n.
b) n 3 - n chia hết cho 6 với mọi số nguyên n.
a) Gợi ý: phân tích 50 n + 2 - 50 n + 1 = 245.10. 50 n .
b) Gợi ý: phân tích n 3 - n = n(n - 1)(n +1).
Đúng 0
Bình luận (0)
chứng minh rằng với mọi n thuộc N* thì n^3 +n+2 là hợp số
n3 + n + 2
= n3 - n + 2n + 2
= n.(n2 - 1) + 2.(n + 1)
= n.(n - 1).(n + 1) + 2.(n + 1)
= (n + 1).(n2 - n + 2), có ít nhất 3 ước khác 1
=> n3 + n + 2 là hợp số với mọi n ϵ N* (đpcm)
Đúng 0
Bình luận (0)
Có: n3 + n + 2 = n(n2+1) + 2
- Nếu n lẻ => n2 lẻ => n2 + 1 chẵn => n2 + 1 chia hết cho 2 => n(n2+1) chia hết cho 2
Mà n(n2+1) + 2 > 2 => n(n2+1) + 2 là hợp số => n3 + n + 2 là hợp số (1)
- Nếu n chẵn => n(n2+1) chia hết cho 2 => n(n2+1) + 2 chia hết cho 2
Mà n(n2+1) + 2 > 2 => n(n2+1) + 2 là hợp số => n3 + n + 2 là hợp số (2)
Từ (1) và (2) => n3 + n + 3 là hợp số với mọi n \(\in\) N*
Đúng 0
Bình luận (2)
chứng minh rằng với mọi n thuộc N* thì n^3 +n+2 là hợp số
Ta có
n3 + n + 2 = (n + 1)(n2 - n + 2)
Ta thấy ( n + 1) > 1
n2 - n + 2 > 1
Vậy n3 + n + 2 luôn chia hết cho 2 số khác 1 nên nó là hợp số
Đúng 0
Bình luận (0)
chứng minh với mọi n là số tự nhiên khác 0 thì n3 + n + 2 là hợp số
Ta có :
n3 + n + 2 = ( n3 + 1 ) + ( n + 1 )
= ( n + 1 ) ( n2 - n + 1 ) + ( n + 1 )
= ( n + 1 ) ( n2 - n + 2 )
Ta thấy n + 1 > 1 ; n2 - n + 2 > 1 nên n3 + n + 2 là hợp số
Đúng 0
Bình luận (0)
Do n là số tự nhiên khác 0 =) n = 2k hoặc 2k + 1 với k là stn
(+) Nếu n = 2k =) n^3 + n + 2 = (2k)^3 + 2k + 2 chia hết cho 2 (1)
(+) Nếu n = 2k + 1 =) n^3 + n + 2 = lẻ + lẻ +chẵn = chẵn chia hết cho 2 (2)
Từ (1) và (2) ta có điều phải chứng minh
Đúng 0
Bình luận (0)
Chứng minh rằng n3 – n chia hết cho 6 với mọi số nguyên n.
A = n3 – n (có nhân tử chung n)
= n(n2 – 1) (Xuất hiện HĐT (3))
= n(n – 1)(n + 1)
n – 1; n và n + 1 là ba số tự nhiên liên tiếp nên
+ Trong đó có ít nhất một số chẵn ⇒ (n – 1).n.(n + 1) ⋮ 2
+ Trong đó có ít nhất một số chia hết cho 3 ⇒ (n – 1).n.(n + 1) ⋮ 3
Vậy A ⋮ 2 và A ⋮ 3 nên A ⋮ 6.
Đúng 0
Bình luận (0)
chứng minh rằng với mọi n thuộc Z và n chẵn thì n3- 4n luôn chia hết cho 48
chứng minh rằng với mọi n thuộc Z và n chẵn thì n3- 4n luôn chia hết cho 48
vì n chẵn nên n= 2m (m thuộc z) => (2m)^3 - 4(2m) chia hết cho 8
mà 8m^3 - 8m = 8m( m^2 -1)= 8 (m-1)m(m+1) do (m-1)m(m+1) là 3 số tự nhiên liên tiếp nên (m-1)m(m+1) chia hết cho 6
vậy 8(m-1)m(m+1) chia hết cho 48
Đúng 0
Bình luận (0)
1. Chứng minh rằng với mọi số tự nhiên n thì ƯCLN(21 4;14 3) 1 n n
2. Chứng minh rằng: Nếu p là số nguyên tố lớn hơn 3 và 2 1 p cũng là số nguyên tố thì 4 1 p
là hợp số?