Chứng minh không tồn tại : abcd-a=2013 abcd-b=213 abcd-c=13 abcd-d=3
CH
Những câu hỏi liên quan
chứng minh rằng không tồn tại các số tự nhiên a,b,c,d nào mà abcd-a=9753;abcd-b=753;abcd-c=53;abcd-d=3
BT9: Chứng minh rằng không tồn tại các số tự nhiên a, b,c nào mà abcd - a = 9753 ; abcd - b = 753 ; abcd -c = 53 ; abcd - d = 3
Tồn tại hay không các số nguyên a, b, c, d sao cho :
abcd – a = 1357 ; abcd – b = 357 ;
abcd – c = 57 ; abcd – d = 7.
Tồn tại hay không các số nguyên a, b, c, d sao cho :
abcd – a = 1357 ;
abcd – b = 357 ;
abcd – c = 57 ;
abcd – d = 7.
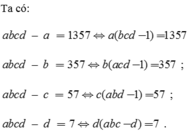
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức)
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài
Đúng 0
Bình luận (0)
Tồn tại hay không các số tự nhiên a,b,c,d thỏa mãn:
abcd-a=1961; abcd-b=961 ;abcd-c= 61; abcd-d=1
khong co stn abcd nao thoa man
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
CMR không tồn tại các số nguyên abcd thỏa mãn đồng thời abcd - a = 9875, abcd- b = 875, abcd- c= 75, abcd- d=5
chứng minh mà, i chả biết không tồn tại, ngu.
Đúng 0
Bình luận (0)
Tồn tại hay không các số nguyên a, b, c, d sao cho
abcd – a = 1357
abcd – b = 357
abcd – c = 57
abcd – d = 7
Đáp án:
Giải thích các bước giải:
Không tồn tại số a,b,c,d
Vì ta có abcd là số có 4 chữ số
abcd-d=7
Số có 4 chữ số - số đơn vị=7( vô lí)
=> không tồn tại a,b,c,d
học tốt
vì abcd là sn có 4 c/s
=> abcd=a000+b00+c0+d
có abcd-d =abc0
=> chữ số cuối cùng của abcd phải là 0 mâu thuẫn với abcd-d=7
=> không tồn tại 4 chữ số nguyên a;b;c;d cần tìm
Chứng tỏ rằng không tồn tại các số nguyên a;b;c;d thỏa mãn đồng thời các hệ thức sau:
abcd - a = 2003 ; abcd - b = 2005
abcd - c = 2007 và abcd - d = 2009
Ta có:
abcd-a=2003
<=>a(bcd-1)=2003
<=>bcd-1=2003/a nguyên (vì bcd-1 nguyên)
suy ra a là ước của 2003
=>a lẻ
Tương tự ta có được b, c, d lẻ
Suy ra abcd lẻ
suy ra (abcd-a) ; (abcd-b)
(abcd-c) ; (abcd-d) đều chẵn
Mâu thuẫn với điều kiện
(2003 ; 2005 ; 2007 ; 2009 đều lẻ)
Vậy không tồn tại a,b,c,d thỏa mãn, thằng Quang ngu
Đúng 0
Bình luận (2)
Đầu nó to \(\Rightarrow\) Cu cũng to
Đúng 0
Bình luận (1)
Bài 1: Có tồn tại cặp số nguyên (a,b) nào thỏa mãn đẳng thức sau không?
a) 42a - 18b = -2018 b)ab(a+b) = -2017
Bài 2: Tồn tại hay không các số nguyên a, b,c, d sao cho abcd -a = -2017, abcd - b= -201 , abcd-c = 399 , abcd - d = -39


