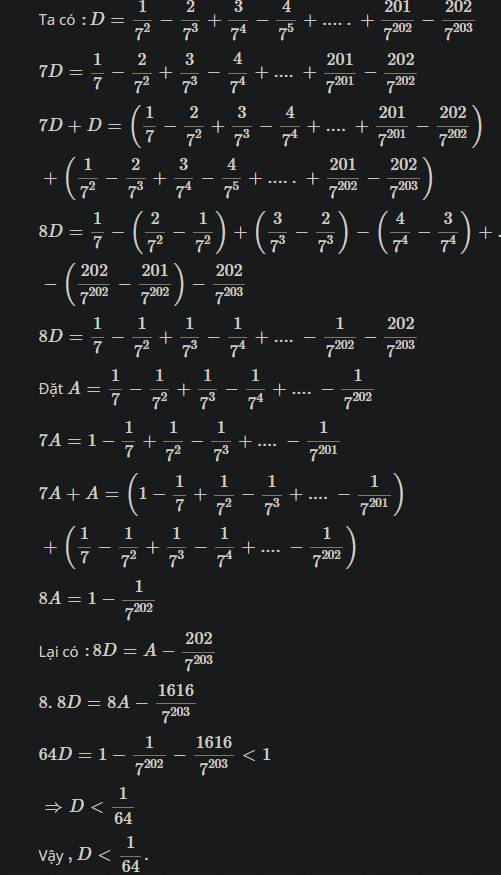So sánh 2301 với 3 201
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PH
Những câu hỏi liên quan
2301 và 2301 So sánh
Xem thêm câu trả lời
93802 : 2301.... 18401 x 287
Hãy so sánh nhé, ai đúng mik tick
là 93802:2301 < 18401 nhân 287 nha
23665445455+123556321+1289?
So sánh:
M= 1/201 + 1/202 + 1/203 + ............. + 1/299 + 1/300
Hãy so sánh M với 1/3
\(M=\frac{1}{201}+\frac{1}{202}+...+\frac{1}{299}+\frac{1}{300}\)
\(\Rightarrow\)Có 100 phân số
Ta có: \(\frac{1}{201}>\frac{1}{300}\)
\(\frac{1}{202}>\frac{1}{300}\)
...................
\(\frac{1}{299}>\frac{1}{300}\)
\(\frac{1}{300}=\frac{1}{300}\)
\(\Rightarrow M>\left(\frac{1}{300}+\frac{1}{300}+...+\frac{1}{300}\right)=\frac{100}{300}=\frac{1}{3}\)
Vậy....
Đúng 0
Bình luận (0)
so sánh 2^201 với 5^79
2201 và 579
2201 = 3.2138761e+60
579 = 1.6543612e+55
Vì 3.2138761e+60 > 1.6543612e+55 nên 2201 > 579
Đúng 0
Bình luận (0)
Cho D = 1/72 - 2/73+3/74-4/75+...+201/7202-202/7203 . Hãy so sánh D với 1/64 .
So sánh: 2^299 và 3^201
Lời giải:
$2^{299}< 2^{300}=(2^3)^{100}=8^{100}$
$3^{201}> 3^{200}=(3^2)^{100}=9^{100}$
$\Rightarrow 3^{201}> 9^{100}> 8^{100}> 2^{299}$
Đúng 0
Bình luận (0)
so sánh 200/201 + 201/202 và 200+201/201+202
\(\frac{200+201}{201+202}=\frac{200}{201+202}+\frac{201}{201+201}\)
Mà \(201\frac{200}{201+202}\)
\(\frac{201}{202}>\frac{201}{201+202}\)
=> \(\frac{200}{201}+\frac{201}{202}>\frac{200+201}{201+202}\)
Đúng 1
Bình luận (0)
So sánh : 200/201+201/202 và (200+201)/(201+202)
\(\frac{200}{201}+\frac{201}{202}=1,99...>1>\frac{401}{403}=\frac{200+201}{201+202}\)
Đúng 0
Bình luận (0)
so sánh
200/201+201/202 và 200+201/201+202
\(\frac{200+201}{201+202}=\frac{200}{201+202}+\frac{201}{201+201}\)
Mà \(201< 201+202\Rightarrow\frac{200}{201}>\frac{200}{201+202}\)
\(\frac{201}{202}>\frac{201}{201+202}\)
Vậy \(\frac{200}{201}+\frac{201}{202}>\frac{200+201}{201+202}\)
Đúng 0
Bình luận (0)