NT
Những câu hỏi liên quan
Tìm mệnh đề phủ định của các mệnh đề sau và xét tính đúng sai của chúng:
a) P : ”∀x ∈ R, ∃y ∈ R : x + y > 0.
b) Q : ”∃x ∈ R, ∀y ∈ R : x + y > 0.
XÉT TÍNH ĐÚNG SAI CỦA MỆNH ĐỀ, GIÚP MK VS Ạ
x4 + y2 ≥ x2y + xy3
Mệnh đề trên SAI.
Rất đơn giản ta thử `x=1,y=2`
`x^4+y^2=5`
`x^2y+xy^3=2+8=10`
`<=>x^2y+xy^3>x^4+y^2`.
Đúng 1
Bình luận (1)
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∀ x ∈ R : x < x + 1
C: “∀ x ∈ R : x < x + 1”.
C− : “∃ x ∈ R: x ≥ x + 1”.
C− sai vì x + 1 luôn lớn hơn x.
Đúng 1
Bình luận (0)
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó ∀ x ∈ R: x.1 = x;
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó. ∀ x ∈ R: x.x = 1
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∃ x ∈ R: 3x = x2 + 1
D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với 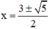
D− thỏa mãn:
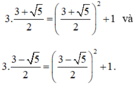
Đúng 0
Bình luận (0)
Phát biểu thành lời, xét tính đúng sai và lập mệnh đề phủ định của các mệnh đề sau:
a/ ∃ x ∈ R : x2 = -1
b/∀ x ∈ R : x2 +x +2 ≠0
giup mình voi . Mình cần gấp
Lời giải:
a. Mệnh đề sai, vì $x^2\geq 0>-1$ với mọi $x\in\mathbb{R}$ theo tính chất bình phương 1 sosos.
Mệnh đề phủ định: $\forall x\in\mathbb{R}, x^2\neq -1$
b. Mệnh đề đúng, vì $x^2+x+2=(x+0,5)^2+1,75>0$ với mọi $x\in\mathbb{R}$ nên $x^2+x+2\neq 0$ với mọi $x\in\mathbb{R}$
Mệnh đề phủ định: $\exists x\in\mathbb{R}| x^2+x+2=0$
Đúng 1
Bình luận (0)
Xét tính đúng sai và viết mệnh đề phủ định của các mệnh đề sau đây:
a) \(\exists x \in \mathbb{N},x + 3 = 0\)
b) \(\forall x \in \mathbb{R},{x^2} + 1 \ge 2x\)
c) \(\forall a \in \mathbb{R},\sqrt {{a^2}} = a\)
a) Mệnh đề sai, vì chỉ có \(x = - 3\) thảo mãn \(x + 3 = 0\) nhưng \( - 3 \notin \mathbb{N}\).
Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{N},x + 3 \ne 0\)”.
b) Mệnh đề đúng, vì \({(x - 1)^2} \ge 0\) hay\({x^2} + 1 \ge 2x\) với mọi số thực x.
Mệnh đề phủ định của mệnh đề này là: “\(\exists x \in \mathbb{R},{x^2} + 1 < 2x\)”
c) Mệnh đề sai, vì có \(a = - 2 \in \mathbb{R},\sqrt {{{( - 2)}^2}} = 2 \ne a\)
Mệnh đề phủ định của mệnh đề này là: “\(\exists a \in \mathbb{R},\sqrt {{a^2}} \ne a\)”.
Đúng 0
Bình luận (0)
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó:
a) \(\forall x \in \mathbb{R},\;{x^2} \ne 2x - 2\)
b) \(\forall x \in \mathbb{R},\;{x^2} \le 2x - 1\)
c) \(\exists x \in \mathbb{R},\;x + \frac{1}{x} \ge 2\)
d) \(\exists x \in \mathbb{R},\;{x^2} - x + 1 < 0\)
a) Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} \ne 2x - 2\)” là mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} = 2x - 2\)”
Mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} = 2x - 2\)” sai vì \({x^2} \ne 2x - 2\)với mọi số thực x ( vì \({x^2} - 2x + 2 = {(x - 1)^2} + 1 > 0\) hay \({x^2} > 2x - 2\)).
b) Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} \le 2x - 1\)” là mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} > 2x - 1\)”
Mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} > 2x - 1\)” đúng vì có \(x = 2 \in \mathbb{R}:{2^2} > 2.2 - 1\) hay \(4 > 3\) (luôn đúng).
c) Phủ định của mệnh đề “\(\exists x \in \mathbb{R},\;x + \frac{1}{x} \ge 2\)” là mệnh đề “\(\forall x \in \mathbb{R},\;x + \frac{1}{x} < 2\)”.
Mệnh đề “\(\forall x \in \mathbb{R},\;x + \frac{1}{x} < 2\)” sai vì \(x = 2 \in \mathbb{R}\) nhưng \(x + \frac{1}{x} = 2 + \frac{1}{2} > 2\).
d) Phủ định của mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} - x + 1 < 0\)” là mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} - x + 1 \ge 0\)”.
Mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} - x + 1 \ge 0\)” đúng vì \({x^2} - x + 1 = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge 0\) với mọi số thực x.
Đúng 0
Bình luận (0)


