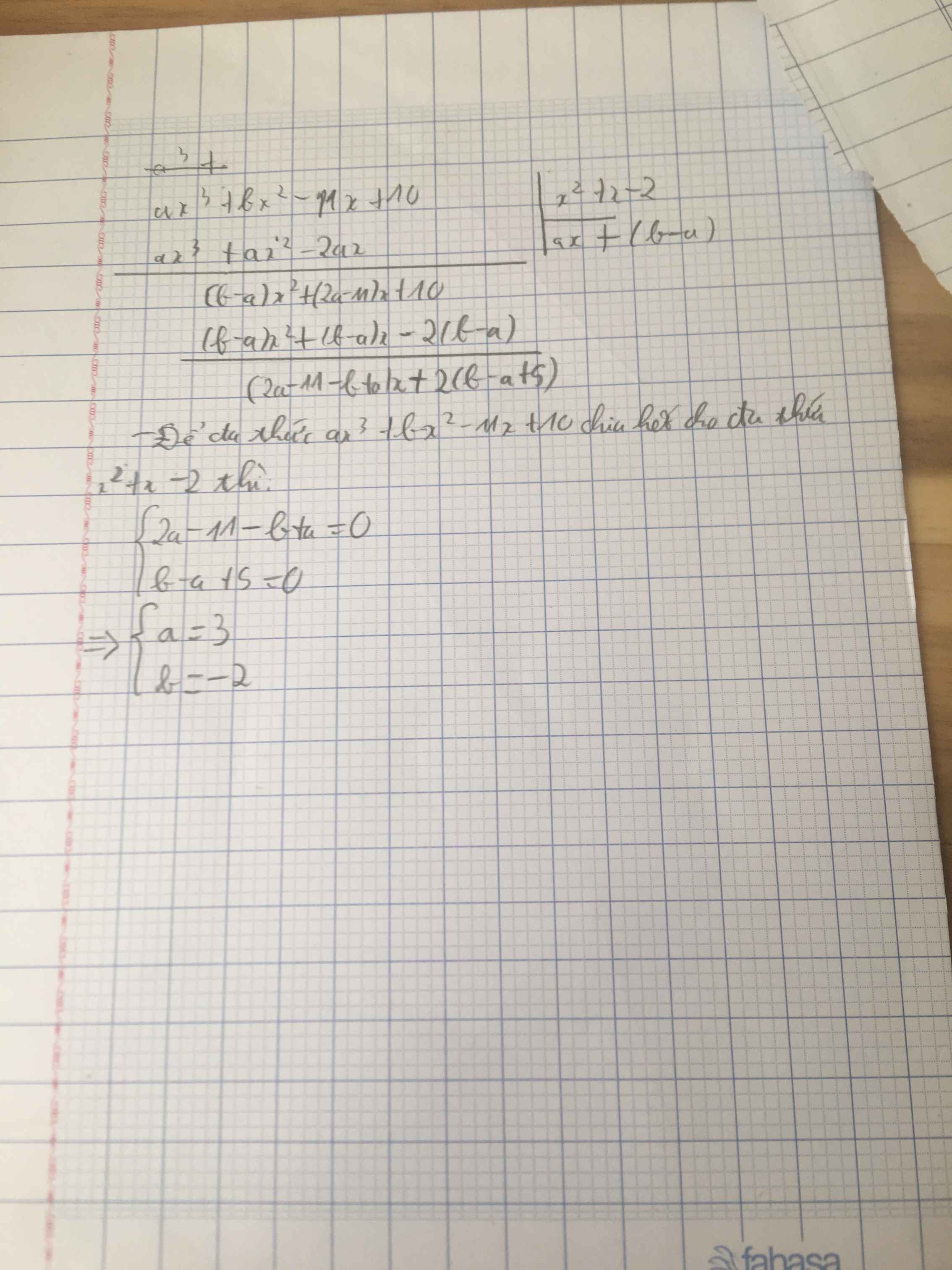xác định hệ số a,b để: ax^3+bx^2-11x+30 chia hết cho x^2-3x-10
DT
Những câu hỏi liên quan
Xác định các số a và b để ax^3+bx^2-11x+30 chia hết cho x^2-3x+10
Xác định hệ số a,b để: ax^3 bx^2-11x 30 chia hết cho x^2-3x-10.
Ai giải đúng và nhanh tick nha
Phần còn lại dành cho bạn ;) Đến đây nắm vững lý thuyết làm oke
Bạn ơi bạn làm nhầm rồi kìa ở phép chia đầu á
xác định số a và b để:
a,ax3+bx2-11x+30 chia hết cho 3x2-2x+1
b,ax4+ bx3+ 1 chia hết cho x2-2x+1
c,x3+ax+b chia x-2 dư 12;chia x+1 dư -6
Xác định a và b để ax3+bx2-11x+30 chia hết cho x2-3x-10
GIẢI DÙM MIK BẰNG CÁCH ĐẶT PHÉP TÍNH
Ta có (ax3 + bx2 - 11x + 30) : (x2 - 3x - 10) = ax + 3a + b (dư (19a +3b - 11)x + 10(b + 3a +3)]
Để (ax3 + bx2 - 11x + 30) \(⋮\) (x2 - 3x - 10) khi \(\hept{\begin{cases}19a+3b-11=0\\b+3a+3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=-9\end{cases}}\)
Vậy a = 2 ; b = -9
Xác định các số a và b để đa thức ax^3+bx^2-11x+10 chia hết cho đa thức x^2+x-2
Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$
$x^2+x-2=(x-1)(x+2)$
Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$
$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức)
$\Leftrightarrow a+b-1=-8a+4b+32=0$
$\Leftrightarrow a=3; b=-2$
Đúng 1
Bình luận (0)
2. Xác định các hằng số a,b, sao cho
a) x^4 + ax^2 + b chia hết cho x^2 -x +1
b) ax^3 + bx^2 + 5x - 50 chia hết cho x^2 + 3x - 10
c) ax^ 3 + bx - 24 chia hết cho ( x+1) ( x+3)
Xác định các hệ số a,b để đa thức \(ax^3+bx^2+5x-50\) chia hết cho đa thức \(x^2+3x-10\) .Đáp án: a=... ; b=....
Tìm hệ số a,b,c để
a) x^3+ax+b chia hết cho x^2+2x -2
b)ax^3+bx^2+5x-50 chia hết cho x^2+3x-10
Mình sẽ làm cách chia nha còn bạn mún cách nào thì bảo mình làm lại
a)
Để \(x^3+ax+b\)chia hết cho \(x^2+2x-2\)
\(\Leftrightarrow\hept{\begin{cases}a+2+4=0\\b-4=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=-6\\b=4\end{cases}}}\)
Vậy \(\hept{\begin{cases}a=-6\\b=4\end{cases}}\)để \(x^3+ax+b\)chia hết cho \(x^2+2x-2\)
Đúng 0
Bình luận (0)
b) dùng phương pháp xét giá trị riêng
Đặt \(f\left(x\right)=ax^3+bx^2+5x-50\)
Ta có: \(f\left(x\right)\)chia hết cho\(x^2+3x-10\)
\(\Rightarrow f\left(x\right)=\left(x^2+3x-10\right).q\left(x\right)\)
\(\Rightarrow f\left(2\right)=\left(2^2+2.3-10\right).q\left(2\right)\)
\(=0\)
\(\Leftrightarrow a.2^3+b.2^2+5.2-50=0\)
\(\Leftrightarrow8a+4b-40=0\)
\(\Leftrightarrow4\left(2a+b-10\right)=0\)
\(\Leftrightarrow2a+b=10\left(1\right)\)
Lai có : \(f\left(-5\right)=\left[\left(-5\right)^2+3.\left(-5\right)-10\right].q\left(-5\right)\)
\(=0\)
\(\Leftrightarrow a.\left(-5\right)^3+b.\left(-5\right)^2+5.\left(-5\right)-50=0\)
\(\Leftrightarrow-125a+25b-25-50=0\)
\(\Leftrightarrow-125a+25b-75=0\)
\(\Leftrightarrow25\left(-5a+b-3\right)=0\)
\(\Leftrightarrow-5a+b=3\left(2\right)\)
Lấy (1) trừ (2) ta được: \(\left(2a+b\right)-\left(-5a+b\right)=10-3\)
\(\Leftrightarrow7a=7\)
\(\Leftrightarrow a=1\)
Thay a=1 vào (1 ) ta được: b=8
Vậy a=1 và b=8
Đúng 0
Bình luận (0)
xác định a, b sao cho
a) x^4 + ax^2 + b chia hết cho x^2 + x + 1
b) ax^3 + bx^2 + 5x chia hết cho x^2 + 3x - 10