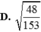Cho tứ diện ABCD; M là điểm nằm trong tam giác ABC;N là điểm nằm trong tam giác ACD. Tìm giao tuyến của các mặt phẳng sau:
a) (AMN) và (BCD)
b) (CMN) và (ABD)
giúp e bài này với em cảm ơn nhiều ạ
Cho tứ diện đều ABCD cạnh a. Tính diện tích mặt cầu nội tiếp tứ diện ABCD
A. πa 2 4
B. πa 2 6
C. Đáp án khác
D. 2 πa 2 3
Cho tứ diện đều ABCD cạnh a. Tính diện tích mặt cầu nội tiếp tứ diện ABCD.
A. 2 πa 2 3
B. πa 2 6
C. πa 2 4
D. Đáp án khác
Cho tứ diện đều ABCD cạnh a. Thể tích của khối tứ diện ABCD là
A. 3 a 3 4
B. 3 a 3 12
C. 2 a 3 12
D. 2 a 3 4
Đáp án C
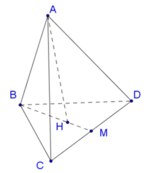
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD.
Ta có A H ⊥ B C D (giả thiết ABCD là tứ diện đều)
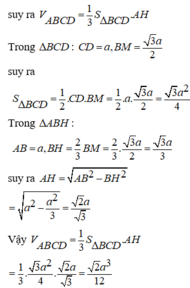
Cho tứ diện đều ABCD cạnh a. Thể tích của khối tứ diện ABCD là
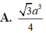
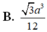
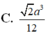
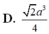
Chọn C
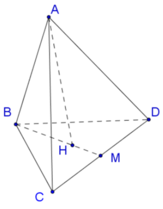
Gọi M là trung điểm của CD, H là trọng tâm của tam giác BCD

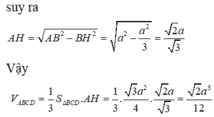
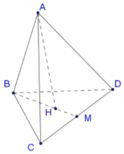
Cho tứ diện đều ABCD cạnh a. Thể tích của khối tứ diện ABCD là
A. 2 a 3 4
B. 2 a 3 12
C. 3 a 3 12
D. 3 a 3 4
Đáp án B
Gọi M là trung điểm của CD , H là trọng tâm của tam giác BCD.
Ta có AH ⊥ BCD (giả thiết ABCD là tứ diện đều) suy ra

Cho khối tứ diện ABCD có thể tích V. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
A. V 27
B. V 18
C. V 4
D. V 12
Đáp án A
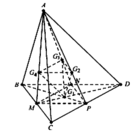
Ta có d G 1 ; G 2 G 3 G 4 = 1 2 d A ; G 2 G 3 G 4
= 1 2 . 2 3 d A ; M N P = 1 3 d A ; M N P S G 2 G 3 G 4 = 2 3 2 S M N P = 4 9 . 1 4 S A B C = 1 9 S A B C
Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
V = 1 3 d G 1 ; G 2 G 3 G 4 . S G 2 G 3 G 4 = 1 3 . 1 3 . d A ; M N P . 1 9 S A B C = 1 27 V A B C D = V 27
Cho khối tứ diện ABCD, M là trung điểm AB. Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện nào?
A. Hai khối lăng trụ tam giác
B. Hai khối chóp tứ giác.
C. Một lăng trụ tam giác và một khối tứ diện
D. Hai khối tứ diện.
Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Tính tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD?
A. 1 4
B. 1 2
C. 1 6
D. 1 8
Đáp án: A.
§ Hướng dẫn giải:
Dễ dàng ta có được
V A B ' C ' D V A B C D = A B ' A B . A C ' A C = 1 4
Cho khối tứ diện ABCD, M là trung điểm của AB. Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện nào?
A. Hai khối lăng trụ tam giác.
B. Hai khối chóp tứ giác.
C. Một khối lăng trụ tam giác và một khối tứ diện
D. Hai khối tứ diện.
Đáp án D
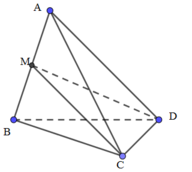
Cách giải:
Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện là: A.MCD và M.BCD
Cho tứ diện đều ABCD có một đường cao A A 1 . Gọi I là trung điểm A A 1 . Mặt phẳng (BCI) chia tứ diện ABCD thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó.
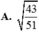
![]()
![]()