Điểm giống và khác nhau của các khối tròn xoay.
PT
Những câu hỏi liên quan
CHỈ RA SỰ GIỐNG VÀ KHÁC NHAU CỦA KHỐI TRÒN XOAY VÀ KHỐI ĐA DIỆN
Khối đa diện là hình được bao bởi đa giác phẳng
Khối tròn xoay là khối hình học được tạo thành khi quay một hình phẳng quanh một đường cố định (trục quay) của hình
Đúng 0
Bình luận (0)
1.Khái niệm,nội dung của bản vẽ chi tiết,bản vẽ lắp,bản vẽ nhà2.Qui ước vẽ ren.3.Các phép chiếu,hình chiếu.4.Hình chiếu,khối đa diện,khối tròn xoay,hình cắt||.Tự luận1.Nội dung,trình tự đọc bản vẽ nhà,bản vẽ chi tiết có ren2.Sự giống nhau và khác nhau trong hình chiếu khối đa diện,khối tròn xoay.3.Phân tích hình dạng khối hình học.4.Vẽ hình chiếu của vật thểCÔNG NGHỆ 8GIÚP MIK VS.ĐAG CẦN GẤP🥴🥴🥴
Đọc tiếp
1.Khái niệm,nội dung của bản vẽ chi tiết,bản vẽ lắp,bản vẽ nhà
2.Qui ước vẽ ren.
3.Các phép chiếu,hình chiếu.
4.Hình chiếu,khối đa diện,khối tròn xoay,hình cắt
||.Tự luận
1.Nội dung,trình tự đọc bản vẽ nhà,bản vẽ chi tiết có ren
2.Sự giống nhau và khác nhau trong hình chiếu khối đa diện,khối tròn xoay.
3.Phân tích hình dạng khối hình học.
4.Vẽ hình chiếu của vật thể
CÔNG NGHỆ 8
GIÚP MIK VS.ĐAG CẦN GẤP🥴🥴🥴
Khái niệm các khối đa diện (hình hộp chữ nhật, hình lăng trụ, hình chóp đều) và các khối tròn xoay (hình trụ, hình nón, hình cầu). Đặc điểm hình chiếu của các khối đa diện và khối tròn xoay.
- Hình hộp chữ nhật là hình được bao bọc bởi sáu hình chữ nhật
- Hình lăng trụ là hình đều được bao bởi 2 mặt đáy là 2 hình đa giác đều bằng nhau và các mặt bên là các hình chữ nhật bằng nhau
-hình chóp đều được bao bởi mặt đáy là một hình đa giác đều và các mặt bên là các hình tam giác cân bằng nhau có chung đỉnh
- Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình trụ
- Khi quay hình tam giác vuông một vòng quay đường kính cố định, ta được hình cầu
- Khi quay tam giác vuông một vòng quanh góc vuông cố định, ta được hình nón
Đúng 2
Bình luận (2)
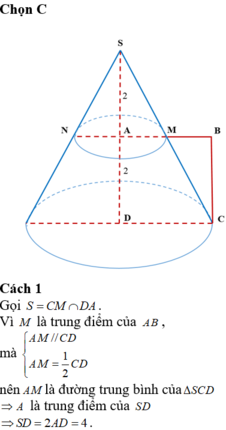
Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Đọc tiếp
Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
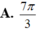
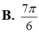
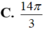
![]()
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo...
Đọc tiếp
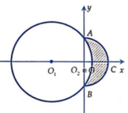
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
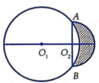
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD, xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường AB. Thể tích của khối tròn xoay đó bằng A.
πa
3
3
B.
3
πa
3
4
C.
7
πa
3...
Đọc tiếp
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD, xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường AB. Thể tích của khối tròn xoay đó bằng
A. πa 3 3
B. 3 πa 3 4
C. 7 πa 3 12
D. 5 πa 3 12
Đáp án D
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
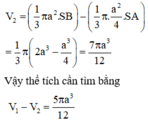
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD, xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường AB. Thể tích của khối tròn xoay đó bằng
Đọc tiếp
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD, xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường AB. Thể tích của khối tròn xoay đó bằng
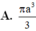
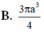
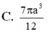
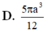
Nêu đặc điểm của các khối tròn xoay?
Đặc điểm hình chiếu của khối tròn xoay là:
- Hình trụ xem hình 1.
- Hình nón xem hình 2.
- Hình cầu xem hình 3.




Đúng 0
Bình luận (0)
Cho hai đường tròn
O
1
;
5
và
O
2
;
5
cắt nhau tại 2 điểm A,B sao cho AB là 1 đường kính của đường tròn
O
2
.
Gọi (D) là hình phẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu...
Đọc tiếp
Cho hai đường tròn O 1 ; 5 và O 2 ; 5 cắt nhau tại 2 điểm A,B sao cho AB là 1 đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ). Quay (D) quanh trục O 1 ; O 2 ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
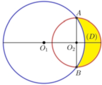
A. V = 36 π .
B. V = 68 π 3 .
C. V = 14 π 3 .
D. V = 40 π 3 .
Đáp án D.
Gắn hệ trục tọa độ Oxy sao cho O 1 ≡ O (gốc tọa độ).
Phương trình đường tròn O 1 ; 5 là x 2 + y 2 = 5 2 ⇒ y = ± 25 − x 2 .
Tam giác O 1 O 2 A vuông tại O 2 , có O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4.
Phương trình đường tròn O 2 ; 3 là x − 4 2 + y 2 = 9 ⇒ y = ± 9 − x − 4 2 .
Gọi V 1 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 1 được giới hạn bởi các đường y = 9 − x − 4 2 , y = 0 , x = 4 , x = 7 quanh trục tung ⇒ V 1 = π ∫ 4 7 9 − x − 4 2 d x .
Gọi V 2 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 2 được giới hạn bởi các đường y = 25 − x 2 , y = 0 , x = 4 , x = 5 quanh trục tung ⇒ V 2 = π ∫ 4 5 25 − x 2 d x .
Khi đó, thể tích cần tính là:
V = V 1 − V 2 = π ∫ 4 7 9 − x − 4 2 d x − π ∫ 4 5 25 − x 2 d x = 40 π 3 .
Đúng 0
Bình luận (0)
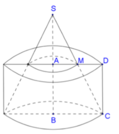
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng A.
5
πa
3
12
B.
3
πa
3
4
C.
7...
Đọc tiếp
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng
A. 5 πa 3 12
B. 3 πa 3 4
C. 7 πa 3 12
D. πa 3 3
Đáp án A
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
Đúng 0
Bình luận (0)