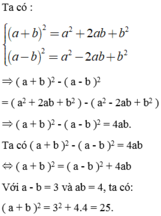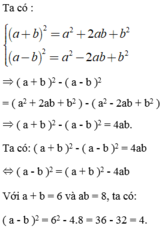Chứng minh : (a-b)^2 = (a+b)^2 -4ab . Tính (a-b)^2009 biết a+b=-3 và a.b=4
HT
Những câu hỏi liên quan
Chứng minh rằng:
(a + b)2 = (a – b)2 + 4ab
(a – b)2 = (a + b)2 – 4ab
Áp dụng:
a) Tính (a – b)2, biết a + b = 7 và a.b = 12.
b) Tính (a + b)2, biết a – b = 20 và a.b = 3.
+ Chứng minh (a + b)2 = (a – b)2 + 4ab
Ta có:
VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab
= a2 + (4ab – 2ab) + b2
= a2 + 2ab + b2
= (a + b)2 = VT (đpcm)
+ Chứng minh (a – b)2 = (a + b)2 – 4ab
Ta có:
VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab
= a2 + (2ab – 4ab) + b2
= a2 – 2ab + b2
= (a – b)2 = VT (đpcm)
+ Áp dụng, tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412.
Đúng 0
Bình luận (0)
Chứng minh rằng :
( a + b )2=(a - b )2 + 4ab
( a - b )2=( a + b )2 - 4ab
Áp dụng
a) Tính ( a - b )2,biết a + b=7 và a.b=12
b) Tính ( a + b)2,biết a - b =20 và a.b=3
Chứng minh: (a+b)2=(a-b)2+4ab ; (a-b)2=(a+b)2-4ab
Áp dụng: a, tínhh (a-b)2 biết a+b=7, a.b=12
b, Tính (a+b)2 biết a-b=20, a.b=3
\(\left(a+b\right)^2=a^2+b^2+2ab=a^2+b^2-2ab+4ab=\left(a-b\right)^2-4ab\)
\(\left(a-b\right)^2=a^2+b^2-2ab=a^2+b^2+2ab-4ab=\left(a-b\right)^2-4ab\)
\(\left(a-b\right)^2=\left(a+b\right)^2-4ab\Rightarrow\left(a-b\right)^2=7^2-4\cdot12=49-48=1\)
\(\left(a+b\right)^2=\left(a-b\right)^2-4ab\Rightarrow\left(a+b\right)^2=20^2-4\cdot3=388\)
Đúng 0
Bình luận (0)
Chứng minh
a) ( a - b )^2 = ( a + b ) - 4ab. Tính ( a - b )^2009 biết a + b = -3 và ab = 4
b) a^3 + b^3 = ( a + b )^3 - 3ab(a + b ). Tính a^3 + b^3 = biết ab = 5 và a + b = -8
c) a^3 - b^3 = ( a - b )^3 + 3ab( a -b ). Tính a^3 - b^3 biết ab = -4 và a - b = 6
d) x^2 - 2xy + y^2 + 1 > 0 với mọi x và y
e) Tính x + y biết x^3 + y^3 = 91 và x^2 - xy + y^2 = 13
Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a - b = 3 và ab = 4.
Chứng minh rằng :
left(a+bright)^2left(a-bright)^2+4ab
left(a-bright)^2left(a+bright)^2-4ab
Áp dụng :
a) Tính left(a-bright)^2, biết a+b7 và a.b12
b) Tính left(a+bright)^2, biết a-b7 và a.b3
Đọc tiếp
Chứng minh rằng :
\(\left(a+b\right)^2=\left(a-b\right)^2+4ab\)
\(\left(a-b\right)^2=\left(a+b\right)^2-4ab\)
Áp dụng :
a) Tính \(\left(a-b\right)^2\), biết \(a+b=7\) và \(a.b=12\)
b) Tính \(\left(a+b\right)^2\), biết \(a-b=7\) và \(a.b=3\)
Bài giải:
a) (a + b)2 = (a – b)2 + 4ab
- Biến đổi vế trái:
(a + b)2 = a2 +2ab + b2 = a2 – 2ab + b2 + 4ab
= (a – b)2 + 4ab
Vậy (a + b)2 = (a – b)2 + 4ab
- Hoặc biến đổi vế phải:
(a – b)2 + 4ab = a2 – 2ab + b2 + 4ab = a2 + 2ab + b2
= (a + b)2
Vậy (a + b)2 = (a – b)2 + 4ab
b) (a – b)2 = (a + b)2 – 4ab
Biến đổi vế phải:
(a + b)2 – 4ab = a2 +2ab + b2 – 4ab
= a2 – 2ab + b2 = (a – b)2
Vậy (a – b)2 = (a + b)2 – 4ab
Áp dụng: Tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4 . 12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4 . 3 = 400 + 12 = 412
Đúng 0
Bình luận (1)
CMR: (a + b)2 = (a - b)2 + 4ab
(a - b)2 = (a + b)2 - 4ab
Ta có: (a + b)2 = a2 + 2ab + b2
= a2 +2ab + b2 - 2ab +2ab
= a2 - 2ab + b2 + 2ab +2ab
= (a - b)2 +4ab
Ta có: (a - b)2 = a2 - 2ab + b2
= a2 - 2ab + b2 + 2ab - 2ab
= a2 + 2ab + b2 - 2ab - 2ab
= (a + b)2 - 4ab
Áp dụng:
a) Tính (a - b)2 , biết a + b = 7 và a.b = 12
Ta có: (a - b)2 = (a + b)2 - 4ab
= 72 - 4.12
= 49 - 48
Vậy (a - b)2 = 1
b) Tính (a + b)2 , biết a - b = 7 và a.b = 3
Ta có: (a + b)2 = (a - b)2 + 4ab
= 72 + 4.3
= 49 + 12
Vậy ( a + b)2 = 61
Đúng 0
Bình luận (0)
\(\left(a+b\right)^2=\left(a-b\right)^2+4ab\)
\(\left(a-b\right)^2+4ab=a^2-2ab+b^2+4ab\)
\(=a^2+2ab+b^2=\left(a+b\right)^2\)
\(\left(a-b\right)^2=\left(a+b\right)^2-4ab\)
\(\left(a+b\right)^2-4ab=a^2+2ab+b^2-4ab\)
\(a^2-2ab+b^2=\left(a-b\right)^2\)
Áp dụng
a)\(\left(a-b\right)^2=\left(a+b\right)^2-4ab\)
\(=7^2-4.12=49-48=1\)
b) \(\left(a+b\right)^2=\left(a-b\right)^2+4ab\)
\(=7^2+4.3=49+12=61\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a + b = 6 và ab = 8
Toán 8 bài 3: Hằng đẳng kiến thức đáng nhớ.
Có (a+b)2 = (a-b)2 +4ab
Tính (a+b), biết a-b=20 và a.b=3.
(a+b)\(^2\)có khác j (a+b)\(^2\)đâu bn
Đúng 0
Bình luận (0)
(a+b)2 = a2+2ab+b2=a2-2ab+4ab+b2=a2-2ab+b2+4ab=(a-b)2+4ab
Đúng 0
Bình luận (0)
Toán 8 bài 3: Hằng đẳng kiến thức đáng nhớ.
Có (a-b)2 = (a+b)2 -4ab
Tính (a-b)2, biết a+b=7 và a.b=12.
Tính ( a - b ) ^ 2, biết a + b = 7 và a . b = 12
Từ đề bài ta có: ( a - b ) ^ 2 = ( a + b ) ^ 2 - 4ab
= ( a - b ) ^ 2 = 7 ^ 2 - 4 . 12
= ( a - b ) ^ 2 = 49 - 48
= ( a - b ) ^ 2 = 1
Vậy ( a - b ) ^ 2 với a + b = 7 và a . b = 12 bằng 1.
Đúng 0
Bình luận (0)