chứng tỏ rằng:
6100-1 chia hết cho 5
2120 - 2110 chia hết cho 2 và 5
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Chứng tỏ rằng 21 10 – 1 chia hết cho 200
* Áp dụng hằng đẳng thức:
![]()
Ta có:
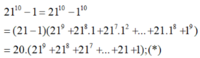
Ta có:
![]()
![]()
gồm có 10 số hạng
![]()
có chữ số tận cùng bằng 0. Do đó, ta có thể viết:
![]()
Thay vào (*) ta được:
2110 - 1 = 20.10.A = 200A
Suy ra: 2110 - 1 chia hết cho 200.
chứng tỏ rằng : a=10! + 1.3.5...9 chia hết cho 5
chứng tỏ rằng : b=10! + 1.3.5...9 + 2009 chia hết cho 2
chứng tỏ rằng : c= 17^17 + 13^13 chia hết cho 2 và 5
chứng tỏ rằng : d= 17^17 - 13^13 chia hết cho 2 nhưng ko chia hết cho 5
a) chứng tỏ rằng 85 +2 11 chia hết cho 17
b)chứng tỏ rằng 8 7-2 18chia hết cho 14
c) chứng tỏ rằng 79 2+79.11 chia hết cho 30
d)chứng tỏ rằng 69 2-69.5 chia hết cho 32
B=3+3 3+3 5+.....+3 1991. chứng minh rằng B chia hết cho 13 và 41
11 n+2+12 20+1 chia hết cho 133
10 28 +8 chia hết cho 72
a) 85+211=23.5+211=211(24+1)=211.17 chia hết cho 17
bài 1:
chứng tỏ rằng :
a, 3mũ2009 - 11mũ50 chia hết cho 2
b,2 mũ 4n+1 + 3 chia het cho 5
bài 3, chứng tỏ rằng A= 2+2mũ2+2mũ3+...+2mũ60 chia hết cho cả 2 và 5
a) Cho các số tự nhiên x ; y. Biết 3x + 2y + 11 chia hết cho 15. Hỏi 18x + 2y + 26 có chia hết cho 15 không? Vì sao?
b) Chứng tỏ rằng 6100 - 1 chia hết cho 5
c) Khi chia một số cho 273 ta được số dư là 182. Hỏi số đó có chia hết cho 91 không? Vì sao?
d) 3 + 32 + 33 + 34 + 35+ 36 + 37 + .... + 360 chia hết cho 4
Câu d là 3 + 32 + 33 + 34 + 35+ 36 + 37 + .... + 360 chia hết cho 4 nhé! Viết vội quá nên quên ![]() , sorry
, sorry
d) (3+32)+(33+34)+(35+36)+...+(359+360)
= 3.(1+3)+33.(1+3)+35.(1+3)+...+359(1+3)
= 3.4+33.4+35.4+...+359.4
= 4.(3+33+35+...+359) chia hết cho 4
Vậy 3+32+33+34+35+36+37+...+360 chia hết cho 4
b) Ta có: 6100-1
= 699.6-1
= 699.(6-1)
= 699.5
Vì 699. 5 chia hết cho 5 nên 6100-1 chia hết cho 5
Vậy 6100-1 chia hết cho 5
A = 119 + 118 +.....+11 + 1 chứng tỏ rằng A chia hết cho 5
B=2 + 22 + 23+ .......+ 220 chứng tỏ rằng B chia hết cho 5
C = 1+ 3+ 32 + ......+ 311 chứng tỏ rằng C chia hết cho 13 và 40
A = 119 + 118 +.....+11 + 1 chứng tỏ rằng A chia hết cho 5
B=2 + 22 + 23+ .......+ 220 chứng tỏ rằng B chia hết cho 5
C = 1+ 3+ 32 + ......+ 311 chứng tỏ rằng C chia hết cho 13 và 40
ta đảo ngược A lại ta có 1+112+113+...+119
2A=112+113+114+....+119+1110
lấy 2A-A còn 1110 có tận cùng băng 0 nên chia hết 5
A = 119 + 118 +.....+11 + 1 chứng tỏ rằng A chia hết cho 5
B=2 + 22 + 23+ .......+ 220 chứng tỏ rằng B chia hết cho 5
C = 1+ 3+ 32 + ......+ 311 chứng tỏ rằng C chia hết cho 13 và 40
Chứng tỏ rằng
a. (10^7+5) chia hết cho 3 và chia hết cho 5
b. (10^m+8) chia hết cho 2 và chia hết cho 9
a ) Ta có :
107 có 7 số 0 và 1 số 1
Nên khi cộng thêm 5 ta có tổng các chữ số là :
1 + 5 = 6\(⋮\)3
Vì : 107 + 5 có số cuối là 5 nên\(⋮\)5
=> 107 + 5\(⋮\)3 và 5
b ) Ta có :
10m + 8 chẵn
=> 10m + 8\(⋮\)2
Ta có :
10m + 8 có tổng\(⋮\)9
=> 10m + 8\(⋮\)2 và 9
a) chứng tỏ rằng a= 9^11+1 chia hết cho cả 2 và 5
b) chứng tỏ rằng a= 9^2n+1chia hết cho 10