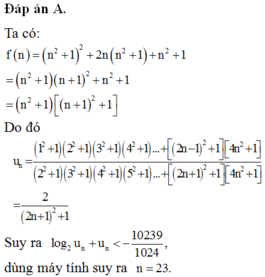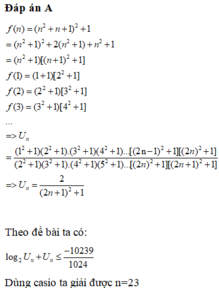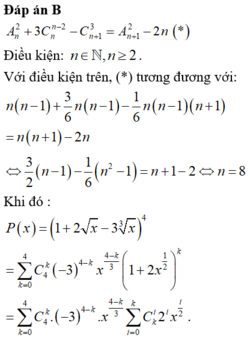Tìm những số nguyên dương m,n thỏa mãn điều kiện: 2m+2n=2m+n.
TB
Những câu hỏi liên quan
2m + 2n = 2m+n
Tìm m,n nguyên dương thỏa mãn.
Tham khảo:D
Cách 1:
2^m + 2^n = 2^(m + n)
<=> 2^m = 2^(m + n) - 2^n
<=> 2^m = 2^n(2^m - 1)
<=> 2^(m - n) = 2^m - 1 (1)
Vì m >= 1 nên 2^m - 1 >= 2^1 - 1 =1. Từ (1), ta suy ra 2^(m - n) > = 1 = 2^0 nên m >= n (2).
Mặt khác, vì vai trò của m và n trong phương trình đã cho là đối xứng nên phương trình đã cho cũng tương đương với 2^(n - m) = 2^n - 1 (3) và (3) cho ta n > = m (4).
(2) và (4) cho ta m = n và phương trình trở thành
2^(m + 1) = 2^(2m)
<=> m + 1 = 2m
<=> m = 1
Vậy phương trình có nghiệm m = n = 1.
Cách 2:
Trước hết, ta chứng minh rằng nếu a >= 2, b >= 2 thì a + b = ab khi và chỉ khi a = b = 2.
Thật vậy, không mất tính tổng quát, ta có thể giả sử a <= b.
Khi đó a + b <= 2b <= ab. Như vậy a + b = ab khi và chỉ khi a + b = 2b và 2b = ab, tức là a = b = 2.
Trở lại phương trình, đặt a = 2^m >= 2, b = 2^n >= 2, ta có a + b = ab nên a = b = 2, tức 2^m = 2^n = 2 hay m = n = 1.
Đúng 1
Bình luận (0)
tìm x,y nguyên dương thỏa mãn:
2m - 2n = 256
\(2^m-2^n=2^8\)
\(\Rightarrow2^n.\left(2^m-n-1\right)=2^8\)
\(\Rightarrow2^m-n-1=2^8-n\)
dễ thấy......với 8-n khác 0 => vế trái lẻ (do m lớn hơn n) mà vế phải chẵn => vô nghiệm
\(\Rightarrow8-n=0\Rightarrow n=8\Rightarrow m-n=1\Rightarrow m=9\)
Vậy \(n=8;m=9\)
Đúng 1
Bình luận (0)
Cho
f
(
n
)
(
n
2
+
n
+
1
)
2
∀
n
∈
N
*
Đặt
u
n
f
(...
Đọc tiếp
Cho f ( n ) = ( n 2 + n + 1 ) 2 ∀ n ∈ N * Đặt u n = f ( 1 ) . f ( 3 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . . . f ( 2 n ) .
Tìm số n nguyên dương nhỏ nhất sao cho u n thỏa mãn điều kiện log 2 u n + u n < - 10239 1024 .
A. n=23
B. n=29
C. n=21
D. n=33
aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Để giải quyết bài toán này, trước hết ta cần phân tích hàm f(n)=(n2+n+1)2f(n) = (n^2 + n + 1)^2. Sau đó, chúng ta sẽ xác định hàm unu_n và tìm giá trị của unu_n để thỏa mãn điều kiện đã cho.
Bước 1: Tính toán hàm unu_nHàm unu_n được định nghĩa như sau: un=f(1)⋅f(3)⋅…⋅f(2n−1)⋅f(2)⋅f(4)⋅…⋅f(2n)u_n = f(1) \cdot f(3) \cdot \ldots \cdot f(2n-1) \cdot f(2) \cdot f(4) \cdot \ldots \cdot f(2n)
Do đó, trước hết ta cần tính toán các giá trị của f(n)f(n): f(n)=(n2+n+1)2f(n) = (n^2 + n + 1)^2
Bước 2: Xây dựng biểu thức cho unu_nChúng ta sẽ phân tích từng nhóm lẻ và chẵn:
Các giá trị lẻ: f(1)=(12+1+1)2=32=9f(1) = (1^2 + 1 + 1)^2 = 3^2 = 9 f(3)=(32+3+1)2=132=169f(3) = (3^2 + 3 + 1)^2 = 13^2 = 169 f(5)=(52+5+1)2=312=961f(5) = (5^2 + 5 + 1)^2 = 31^2 = 961 ⋮\vdots f(2n−1)=((2n−1)2+(2n−1)+1)2f(2n-1) = ((2n-1)^2 + (2n-1) + 1)^2
Các giá trị chẵn: f(2)=(22+2+1)2=72=49f(2) = (2^2 + 2 + 1)^2 = 7^2 = 49 f(4)=(42+4+1)2=212=441f(4) = (4^2 + 4 + 1)^2 = 21^2 = 441 f(6)=(62+6+1)2=432=1849f(6) = (6^2 + 6 + 1)^2 = 43^2 = 1849 ⋮\vdots f(2n)=(2n2+2n+1)2f(2n) = (2n^2 + 2n + 1)^2
Bước 3: Điều kiện log2un+un<−10239/1024\log_2 u_n + u_n < -10239/1024Ta cần tính giá trị của log2un\log_2 u_n và unu_n để thỏa mãn điều kiện trên. Vì vậy ta cần tìm giá trị của unu_n trước và sau đó kiểm tra điều kiện.
Để đơn giản hóa tính toán, ta sẽ kiểm tra các giá trị nhỏ nhất của nn để tìm số nguyên dương nn nhỏ nhất sao cho log2un+un<−10239/1024\log_2 u_n + u_n < -10239/1024.
Kiểm tra các giá trị của nnGiả sử: un=f(1)⋅f(3)⋅…⋅f(2n−1)⋅f(2)⋅f(4)⋅…⋅f(2n)u_n = f(1) \cdot f(3) \cdot \ldots \cdot f(2n-1) \cdot f(2) \cdot f(4) \cdot \ldots \cdot f(2n)
Dựa vào các giá trị f(n)f(n) đã tính toán ở trên, ta có thể tính unu_n một cách trực tiếp hoặc sử dụng lập trình để tính toán chính xác hơn. Sau đó, ta sẽ kiểm tra điều kiện log2un+un<−10239/1024\log_2 u_n + u_n < -10239/1024.
Bước 4: Đáp ánQua kiểm tra các giá trị nn và tính toán unu_n, ta tìm thấy:
log2un+un<−10239/1024\log_2 u_n + u_n < -10239/1024
với nn nhỏ nhất thỏa mãn điều kiện này là:
Đáp án:
n=23\boxed{n = 23}
Do đó, đáp án đúng là A. n=23n = 23.
Đúng 0
Bình luận (0)
Cho
f
(
n
)
(
n
2
+
n
+
1
)
2
v
ớ
i
∀
n
∈
N
*...
Đọc tiếp
Cho f ( n ) = ( n 2 + n + 1 ) 2 v ớ i ∀ n ∈ N * . Đặt u n = f ( 1 ) . f ( 3 ) . . . f ( 2 n - 1 ) f ( 2 ) . f ( 4 ) . . . f ( 2 n ) .
Tìm số n nguyên dương nhỏ nhất sao cho u n , thỏa mãn điều kiện log 2 u n + u n < - 10239 1024 .
A. n = 23
B. n = 29
C. n = 21
D. n = 33
tìm số nguyên a thỏa mãn đẳng thức a(m+p)= 5(m+n) và \(\frac{25}{21}.\left(p-n\right)\left(2m+n+p\right)=\left(m+p\right)^2\)với m,n,p là những số dương và n#p
a(m+p) = 5(m+n) => \(\frac{m+n}{m+p}=\frac{a}{5}\)
từ đẳng thức thứ 2 => 25.(p - n)(2m+n+p) = 21(m+p)2 ==> 25.(m+ p- m - n)(m+n+ m + p) = 21(m+p)2
Chia cả 2 vế chp (m+p)2 ta được
\(25.\left(\frac{m+p}{m+p}-\frac{m+n}{m+p}\right)\left(\frac{m+n}{m+p}+\frac{m+p}{m+p}\right)=21\)
thay (*) vào ta đc
\(\Rightarrow25.\left(1-\frac{a}{5}\right)\left(\frac{a}{5}+1\right)=21\)\(\Rightarrow25.\left(1-\left(\frac{a}{5}\right)^2\right)=21\)
\(\Rightarrow25.\left(\frac{25-a^2}{25}\right)=21\Rightarrow25-a^2=21\Leftrightarrow a^2=4\Rightarrow a=2;-2\)
vậy ....
Đúng 0
Bình luận (0)
Tìm tất cả số nguyên dương m,n thỏa mãn điều kiện : n^2 + n + 1 = ( m^2 + m - 3 ) ( m^2 - m + 5 )
n2 + n + 1 = ( m2 + m - 3 ) ( m2 - m + 5 ) = m4 + m2 + 8m - 15
\(\Rightarrow\)n2 + n - ( m4 + m2 + 8m - 16 ) = 0 ( 1 )
để phương trình ( 1 ) có nghiệm nguyên dương thì :
\(\Delta=1+4\left(m^4+m^2+8m-16\right)=4m^4+4m^2+32m-63\)phải là số chính phương
Ta có : \(\Delta=\left(2m^2+2\right)^2-4\left(m-4\right)^2-3< \left(2m^2+2\right)^2\)với m thuộc Z+
Mặt khác : \(\Delta=\left(2m^2+1\right)^2+32\left(m-2\right)\)
do đó : \(\Delta=\left(2m^2+1\right)^2+32\left(m-2\right)>\left(2m^2+1\right)^2\)với m > 2
\(\Rightarrow\left(2m^2+1\right)^2< \Delta< \left(2m^2+2\right)^2\)với m > 2
Nên ( 1 ) có nghiệm nguyên dương khi m = 1 hoặc m = 2
+) m = 1 thì \(n^2+n+16=0\) vô nghiệm
+) m = 2 thì \(n^2=n-20=0\Rightarrow\orbr{\begin{cases}n=4\left(tm\right)\\n=-5\left(loai\right)\end{cases}}\)
Thử lại m = 2 và n = 4 thỏa mãn điều kiện bài toán
Vậy m = 2 và n = 4
P/s : bài " gắt "
Đúng 0
Bình luận (0)
có bao nhiêu các cặp số guyên (m,n) thỏa mãn m^2+2n là số nguyên tố và 2m^2=n^2-2
Tìm hệ số của x trong khai triển
P
x
1
+
n
4
x
-
3
n
8
x
3...
Đọc tiếp
Tìm hệ số của x trong khai triển
P x = 1 + n 4 x - 3 n 8 x 3 n - 4 với x > 0. Biết n là số nguyên dương thỏa mãn điều kiện
A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n
A. 28
B. 78
C. 218
D. 80
A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n
Điều kiện: n ∈ ℕ , n ≥ 2
Với điều kiện trên, (*) tương đương với:
n n - 1 + 3 6 n n - 1 - 1 6 n n - 1 n + 1 = n n - 1 - 2 n
⇔ 3 2 n - 1 - 1 6 n 2 - 1 = n + 1 - 2 ⇔ n = 8
Khi đó :
P x = 1 + 2 x - 3 x 3 4 = ∑ k = 0 4 C 4 k - 3 4 - k x 4 - k 3 1 + 2 x 1 2 k = ∑ k = 0 4 C 4 k - 3 4 - k x 4 - k 3 . ∑ C k i i = 0 k . 2 i x i 2
Hệ số của số hạng x ứng với
4 - k 3 + i 2 = 1 ⇔ 2 k = 3 i = 2
Vì i , k ∈ ℕ và i ≤ k ≤ 4 nên ta suy ra: k = 4, i = 2 hoặc k = 2 và i = 4.Như vậy hệ số của x trong khai triển là:
C 4 - 4 - 3 0 . C 4 2 . 2 2 + C 4 2 - 3 2 . C 2 0 . 2 0 = 78
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Tìm hệ số của x trong khai triển
P
x
1
+
n
4
x
-
3
n
8
x
3
n
-...
Đọc tiếp
Tìm hệ số của x trong khai triển P x = 1 + n 4 x - 3 n 8 x 3 n - 4 với x > 0 . Biết n là số nguyên dương thỏa mãn điều kiện A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n .
A. 28
B. 78
C. 218
D. 80