cho 3 đường thẳng a b c phân biệt chứng minh rằng a//b a//c chứng minh rằng b//c
NL
Những câu hỏi liên quan
cho 4 đường thẳng phân biệt a,b,c,d. Vẽ đường thẳng a vuông góc với b, vẽ b vuông góc với c và vẽ c vuông góc với d. Chứng minh rằng a vuông góc với d
b vuông góc với c và c vuông góc với d
nên b song song với d (1)
mà a vuông góc với b (2)
từ 1;2 suy ra a vuông góc với d
Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.
THAM KHẢO:
Vì AB và AC cùng vuông góc với một mặt phẳng (P) nên AB trùng AC
⇒⇒ A, B, C thẳng hàng.
Đúng 1
Bình luận (0)
Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b taij hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong giao tuyến của hai mặt phẳng (ABM) và (SCD).
Tham khảo:
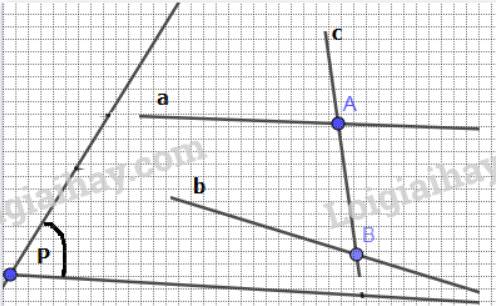
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B
Ta có A thuộc a mà a nằm trong mp(P) suy ra A cũng nằm trong mp(P)
B thuộc b mà b nằm trong mp(P) suy ra B cũng nằm trong mp(P)
Suy ra đường thẳng AB cũng nằm trong mp(P) tức c cũng nằm trong mp(P).
Đúng 0
Bình luận (0)
Cho a,b,c là 3 đường thẳng phân biệt. Chứng minh nếu a // c, b // c thì a // b
Cho ABC có A = 60độ , kẻ tia phân giác của góc B cắt AC ở D, tia phân giác góc C cắt AB ở E.
Qua A kẻ đường thẳn song song với CE, đường thẳng này cắt đường thẳng BC tại F.
a) Chứng minh rằng: AFC = CAF
b) Chứng minh rằng: BDC = AEC
Cho tam giác ABC có góc A = 600, kẻ tia phân giác của góc B cắt AC ở D, tia phân giác góc C cắt AB ở E. Qua A kẻ đường thẳng song song với CE, đường thẳng này cắt đường thẳng BC tại E. a. Chứng minh rằng góc AFC = CAF b. Chứng minh rằng góc BDC = AEC
cho mặt phẳng (P) và 3 điểm phân biệt A , B , C cùng nằm ngoài (P) . chứng minh rằng nếu 3 đường thẳng AB , BC , CA cùng cắt mặt phẳng (P) thì các giao điểm đó thẳng hàng .
Cho 4 số nguyên phân biệt a,b,c,d. Chứng minh rằng : (a-b)(a-c)(a-d)(b-c)(b-d)(c-d) chia hết cho 12
Lời giải:
Có 44 số a,b,c,da,b,c,d và 33 số dư có thể xảy ra khi chia một số cho 33 là 0,1,20,1,2
Do đó áp dụng nguyên lý Dirichlet tồn tại ít nhất [43]+1=2[43]+1=2 số có cùng số dư khi chia cho 3
Không mất tổng quát giả sử đó là a,b⇒a−b⋮3a,b⇒a−b⋮3
⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮3⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮3
Mặt khác:
Trong 4 số a,b,c,da,b,c,d
Giả sử tồn tại hai số có cùng số dư khi chia cho 44 là a,ba,b
⇒a−b⋮4⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮4⇒a−b⋮4⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮4
Nếu a,b,c,da,b,c,d không có số nào có cùng số dư khi chia cho 4. Khi đó giả sử a,b,c,da,b,c,d có số dư khi chia cho 44 lần lượt là 0,1,2,30,1,2,3
⇒c−a⋮2;d−b⋮2⇒c−a⋮2;d−b⋮2
⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮4⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮4
Như vậy, tích đã cho vừa chia hết cho 3 vừa chia hết cho 4. Do đó no cũng chia hết cho 12
Đúng 0
Bình luận (0)
Cho 4 số nguyên phân biệt a,b,c,d. Chứng minh rằng : (a-b)(a-c)(a-d)(b-c)(b-d)(c-d) chia hết cho 12
Giải
Không mất tổng quát giả sử đó là a,b⇒a−b⋮3
⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮3
Mặt khác:
Trong 4 số a,b,c,d
Giả sử tồn tại hai số có cùng số dư khi chia cho 4 là a,b
⇒a−b⋮4⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮4
Nếu a,b,c,d không có số nào có cùng số dư khi chia cho 4. Khi đó giả sử a,b,c,d có số dư khi chia cho 4 lần lượt là 0,1,2,3
⇒c−a⋮2;d−b⋮2
⇒(b−a)(c−a)(d−a)(d−c)(d−b)(c−b)⋮4
Như vậy, tích đã cho vừa chia hết cho 3 vừa chia hết cho 4. Do đó no cũng chia hết cho 12
Ta có đpcm,
Đúng 0
Bình luận (0)
Cho tam giác ABC và M là trung điểm của AB . Qua M kẻ đường thẳng a//BC. Qua C kẻ đường thẳng b//AB. Đường thẳng a cắt AC tại N. Đường thẳng a cắt đừong thẳng b tại D.
a) Nối M và C. Chứng minh rằng MBC = CDM. Từ đó, hãy suy ra MB = CD và MD = BC;
b) Chứng minh rằng AMN = CDN.
c) Chứng minh rằng NA = NC và MN = 1/2 BC.




