Tính giá trị biểu thức : M = xyz + x2y2z2+x3y3z3+ ... + x100y100z100, biết x= -1: y= -1: z= -1
YC
Những câu hỏi liên quan
Tính giá trị của các đa thức sau: xyz + x2y2z2 + x3y3z3 + ….. + x10y10z10 tại x = 1; y = -1; z = -1
Ta có: xyz + x2y2z2 + x3y3z3 + ….. + x10y10z10
= xyz + (xyz)2 + (xyz)3 + ….. + (xyz)10
Với x = 1; y = -1; z = - 1 ta có: xyz = 1.(-1).(-1) = 1
Thay vào đa thức: 1 + 12 + 13 + … + 110 = 10
Đúng 0
Bình luận (0)
câu 1 : tính giá trị biểu thức (x+y)(y+z)(z+x) biết x+y+z=0 và xyz=2010
câu 2: tính giá trị biểu thức 3x^7 - 5y^6 +1 tại x,y biết rằng : (x+1)^2010 + (y-1)^2000=0
cho x, y,z đều khác 0 thỏa mãn x+y+z=xyz và1/x+1/y+1/z=căn 3
Tính giá trị biểu thức: M=1/x^2+1/y^2+1/z^2
Cho xyz khác 0 thỏa mãn: x^3y^3 + y^3z^3 + z^3x^3 = 3x^2y^2z^2
Tính giá trị của biểu thức: M = ( 1+ x/y )( 1 + y/z )( 1 + z/x )
3x²y²z² = x³y³ y³z³ z³x³
(3x²y²z²) / (x³y³ y³z³ z³x³) = 1
3.[(x²y²z²) / (x³y³ y³z³ z³x³)] = 1
(x²y²z²) / (x³y³ y³z³ z³x³) = 1/3
(x²y²z²) / (x³y³) (x²y²z²) / (y³z³) (x²y²z²) / (z³x³) = 1/3
z²/(xy) x/(yz) y²/(zx) = 1/3
Vậy x²/(yz) y²/(xz) z²/(xy) = 1/3
Đúng 0
Bình luận (0)
Tính giá trị các biểu thức sau tại x = 1; y = -1; z = 3. xyz + 2 x 2 y y 2 + 1
Thay x = 1; y = -1; z = 3 vào biểu thức, ta có:
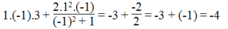
Vậy giá trị của biểu thức xyz + 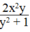 bằng -4 tại x = 1; y = -1; z = 3
bằng -4 tại x = 1; y = -1; z = 3
Đúng 0
Bình luận (0)
Cho xyz=1,tính giá trị biểu thức 1/(1+x+xy)+1/(1+y+yz)+1/(1+z+zx)
Xem chi tiết
\(\dfrac{1}{1+x+xy}+\dfrac{1}{1+y+yz}+\dfrac{1}{1+z+zx}\)
\(=\dfrac{1}{1+x+xy}+\dfrac{x}{x+xy+xyz}+\dfrac{xy}{xy+xyz+xyzx}\)
\(=\dfrac{1}{1+x+xy}+\dfrac{x}{x+xy+1}+\dfrac{xy}{xy+1+x}\) (Do xyz = 1)
\(=1\).
Đúng 0
Bình luận (0)
1, Tính giá trị biểu thức sau tại x+y+1=0
D= x²(x+y) - y²(x+y) + x² - y² + 2(x+y) + 3
2, Cho xyz=2 và x+y+z=0
Tính giá trị biểu thức
M= (x+y)(y+z)(x+z)
TLMJFDLIIS HFIEHFU ưAUDSEIq
1, Tính giá trị biểu thức sau tại x+y+1=0
\(D=x^2\left(x+y\right)-y^2\left(x+y\right)+x^2-y^2+2\left(x+y\right)+3\left(1\right)\)
Ta có: x + y + 1 = 0 => x + y = -1
(1) \(\Leftrightarrow x^2.\left(-1\right)-y^2.\left(-1\right)+\left(x-y\right)\left(x+y\right)+2.\left(-1\right)+3\)
\(=y^2-x^2+\left(x-y\right)\left(-1\right)-2+3\)
\(=\left(y-x\right)\left(y+x\right)-\left(x-y\right)+1\)
\(=\left(y-x\right).\left(-1\right)-x+y+1\)
\(=-y+x-x+y+1\)
\(=1\)
2, Cho xyz=2 và x+y+z=0
Tính giá trị biểu thức
\(M=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Ta có: x + y + z = 0
=> x + y = -z (1)
=> y + z = -x (2)
=> x + z = -y (3)
Từ (1);(2);(3)
=> \(M=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)<=> (-z).(-x).(-y) = 0
1, x+y+z=1
\(D=x^2\left(x+y\right)-y^2\left(x+y\right)+x^2-y^2+2\left(x+y\right)+3\)
\(=\left(x+y\right)\left(x^2-y^2+2\right)+x^2-y^2+3\)
\(=\left(x+y\right)\left(x^2-y^2+2\right)+\left(x^2-y^2+2\right)+1\)
\(=\left(x^2-y^2+2\right)\left(x+y+1\right)+1\)
=1 (vì x+y+1=0)
2, x+y+z=0 <=> \(\hept{\begin{cases}x=-\left(y+z\right)\\y=-\left(x+z\right)\\z=-\left(x+y\right)\end{cases}}\)
Nhân theo vế ta được: xyz=\(-\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Rightarrow2=-\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
=> (x+y)(y+z)(z+x)=-2
Xem thêm câu trả lời
Tính giá trị của biểu thức:\(A=\frac{x}{xy+x+1}+\frac{y}{y+1+yz}+\frac{z}{1+z+xz}\)
biết \(xyz=1\)
\(A=\frac{x}{xy+x+1}+\frac{y}{y+1+yz}+\frac{z}{1+z+xz}\)
\(=\frac{x}{xy+x+1}+\frac{xy}{xy+x+xyz}+\frac{xyz}{xy+xyz+x^2yz}\)
\(=\frac{x}{xy+x+1}+\frac{xy}{xy+x+1}+\frac{1}{xy+1+x}\)
\(=\frac{xy+x+1}{xy+x+1}=1\)
Đúng 0
Bình luận (0)
\(\frac{x}{xy+x+1}+\frac{xy}{yx+x+xyz}+\frac{xyz}{xy+xyz+x^2yz}\)
\(\frac{x}{xy+x+1}+\frac{xy}{yx+x+1}+\frac{1}{xy+1+x}\)
\(\frac{x+xy+1}{xy+x+1}=1\)
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức A = \(\left(1+\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\left(1+\frac{z}{x}\right)\) biết x+y+z=0 và xyz khác 0
Ta có :
\(A=\left(1+\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\left(1+\frac{z}{x}\right)\)
\(=\frac{x+y}{y}.\frac{y+z}{z}.\frac{z+x}{x}\)
Do x + y + z = 0 => x+y = -z ; y+z = -x ; z+x = -y
\(\Rightarrow A=\frac{-z}{y}.\frac{-x}{z}.\frac{-y}{x}=\frac{\left(-1\right).xyz}{xyz}=-1\)
Cho \(x,y,z\in Q\) sao cho \(xyz=1\)
Tính giá trị của biểu thức \(A=\dfrac{1}{xy+x+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\) ?
\(A=\dfrac{1}{xy+x+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{1}{xy+x+xyz}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{1}{x\left(y+1+yz\right)}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{xyz}{x\left(y+1+yz\right)}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz}{y+1+yz}+\dfrac{1}{y+yz+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz+1}{y+1+yz}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz+xyz}{y+xyz+yz}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{y\left(z+xz\right)}{y\left(1+xz+z\right)}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{z+xz+1}{xz+z+1}\)
\(A=1\)
Đúng 3
Bình luận (1)
\(A=\dfrac{1}{xy+x+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)⇔\(A=\dfrac{z}{1+xz+z}+\dfrac{xz}{z+1+xz}+\dfrac{1}{xz+z+1}\)(vì xyz=1)
⇔\(A=\dfrac{z+xz+1}{xz+z+1}\)⇔\(A=1\)
Xong rồi nè bn ơi ![]()
Đúng 0
Bình luận (0)
\(\dfrac{1}{xy+x+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(=\dfrac{1}{\dfrac{1}{z}+\dfrac{1}{yz}+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{\dfrac{1}{y}+z+1}\)
\(=\dfrac{1}{\dfrac{y+1+yz}{yz}}+\dfrac{1}{yz+y+1}+\dfrac{1}{\dfrac{1+zy+y}{y}}\)
\(=\dfrac{yz}{y+1+yz}+\dfrac{1}{yz+y+1}+\dfrac{y}{1+zy+y}=\dfrac{y+yz+1}{y+yz+1}=1\)
Đúng 1
Bình luận (0)






