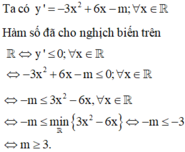Tìm tất cả các giá trị thực của tham số m để hàm số y=sinx-mx nghịch biến trên R
HD
Những câu hỏi liên quan
Cho hàm số
y
sin
x
-
3
cos
x
-
m
x
. Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R A.
m
≤
-
2
B.
m
≤
-
3
C.
m
≥
2
D.
m
≥
1
Đọc tiếp
Cho hàm số y = sin x - 3 cos x - m x . Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R
A. m ≤ - 2
B. m ≤ - 3
C. m ≥ 2
D. m ≥ 1
Cho hàm số ysinx-
3
cosx-mx Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R. A. B.m2 C. D.
Đọc tiếp
Cho hàm số y=sinx- 3 cosx-mx Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R.
A.![]()
B.m>2
C.![]()
D.![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
s
i
n
x
−
m
x
nghịch biến trên R A.
m
1
B.
m
−
1
C.
m
1
D.
m
≥
1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = s i n x − m x nghịch biến trên R
A. m < 1
B. m > − 1
C. m > 1
D. m ≥ 1
Đáp án D
Ta có y ' = cos x − m .
Hàm số nghịch biến trên R
⇔ y ' ≤ 0 , ∀ x ∈ ℝ ⇒ cos x − m ≤ 0 ∀ x ∈ ℝ ⇔ cos x ≤ m ∀ x ∈ ℝ ⇒ m ≥ M a x ℝ cos x = 1.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số ysinx+cosx+mx đồng biến trên khoảng
-
∞
;
+
∞
A
.
-
2
≤
m
≤
2
B
.
m
≤
-
2
C
.
-
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=sinx+cosx+mx đồng biến trên khoảng - ∞ ; + ∞
A . - 2 ≤ m ≤ 2
B . m ≤ - 2
C . - 2 < m < 2
D . m ≥ 2
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y sinx+ cosx+ mx đồng biến trên
ℝ
A. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx+ cosx+ mx đồng biến trên ℝ
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y sinx + cosx + mx đồng biến trên
ℝ
A.
-
2
≤
m
≤
2
B.
m
≤
-
2
C.
-
2
m
2
D.
m
≥
2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx + cosx + mx đồng biến trên ℝ
A. - 2 ≤ m ≤ 2
B. m ≤ - 2
C. - 2 < m < 2
D. m ≥ 2
Đáp án D
YCBT: y ' = cos x - sin x + m ≥ 0 với mọi x ∈ ℝ ⇔ m ≥ sin x - cos x = f x với x ∈ ℝ .
Mà ta có: f x = sin x - cos x = 2 x - π 4 ⇒ - 2 ≤ f x ≤ 2 ⇒ m ≥ 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
x
+
4
x
+
m
nghịch biến trên khoảng
−
∞
;
1
. A.
−
2
m
≤
−
1
B.
−...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x + 4 x + m nghịch biến trên khoảng − ∞ ; 1 .
A. − 2 < m ≤ − 1
B. − 2 ≤ m ≤ − 1
C. − 2 ≤ m < − 1
D. − 2 < m < 1
Tìm tất cả các giá trị thực của tham số m để hàm số
y
−
x
3
+
3
x
2
−
m
x
+
m
nghịch biến trên
ℝ
A.
m
≤
3
B. m 3 C.
m
≥
3
D. m 3
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = − x 3 + 3 x 2 − m x + m nghịch biến trên ℝ
A. m ≤ 3
B. m < 3
C. m ≥ 3
D. m < 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
x
+
4
x
+
m
nghịch biến trên khoảng
−
∞
;
1
. A.
−
2
m
≤
−
1
B.
−
2
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x + 4 x + m nghịch biến trên khoảng − ∞ ; 1 .
A. − 2 < m ≤ − 1
B. − 2 ≤ m ≤ − 1
C. − 2 ≤ m < − 1
D. − 2 < m < 1
Đáp án A.
Tập xác định: D = ℝ \ − m . Ta có y ' = m 2 − 4 x + m 2 .
Để hàm số nghịch biến trên khoảng − ∞ ; 1 thì ta phải có
m 2 − 4 < 0 1 ≤ − m ⇔ − 2 < m < 2 m ≤ − 1 ⇔ − 2 < m ≤ − 1
Lưu ý: Với cách cho đáp án như trong câu hỏi này, ta có làm như sau:
- Thử với m = − 2 . Khi đó y = − 2 x + 4 x − 2 = − 2 x − 2 x − 2 = − 2 . Suy ra với m = − 2 thì hàm số không nghịch biến trên − ∞ ; 1 . Từ đó loại được đáp án B và C.
- Thử với m = − 1 . Khi đó y = − x + 4 x − 1 . Ta có y ' = − 3 x − 1 2 < 0 ∀ x ≠ 1 .
Suy ra hàm số nghịch biến trên các khoảng − ∞ ; 1 và 1 ; + ∞ . Vậy A là đáp án đúng.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để trên
(
-
1
;
1
)
hàm số
y
m
x
+
6
2
x
+
m
+
1
nghịch biến A.
-
4
m
3
B....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để trên ( - 1 ; 1 ) hàm số y = m x + 6 2 x + m + 1 nghịch biến
A. - 4 < m < 3
B. - 4 ≤ m < - 3 1 < m ≤ 3
C. 1 ≤ m < 4
D. - 4 < m ≤ - 3 1 ≤ m < 3