biết x2+y2+z2-2x+4y-6z=-14
khi đó x+y+z=
NH
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho
(
a
)
:
2
x
−
2
y
−
z
+
14
0
, mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
−
4
y
−
6
z
−
11...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ( a ) : 2 x − 2 y − z + 14 = 0 , mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x − 4 y − 6 z − 11 = 0 . Mặt phẳng (P)//(a) cắt (S) theo thiết diện là một hình tròn có diện tích 16 π . Khi đó phương trình mặt phẳng (P) là:
A. 2 x − 2 y − z + 14 = 0
B. 2 x − 2 y − z + 4 = 0
C. 2 x − 2 y − z + 16 = 0
D. 2 x − 2 y − z − 4 = 0
Đáp án D.
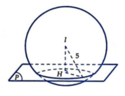
(P )//( α ) ⇒ ( P ) : 2 x − 2 y − z + c = 0 (c ≠ 14)
(S) có tâm I ( 1 ; 2 ; 3 ) , bán kính R=5
Hình tròn thiết diện (C) có S = 16 π =>Bán kính r = 4
Gọi H là hình chiếu của I lên (P) =>H là tâm của (C)
⇒ I H = d ( I ; ( P ) ) = R 2 − r 2 = 3
⇒ 2.1 − 2.2 − 3 + c 2 2 + 2 2 + 1 2 = 3 ⇔ c − 5 = 9 ⇔ c = 14 ( 1 ) c = − 4 ⇒ ( P ) : 2 x − 2 y − z − 4 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho
(
a
)
:
2
x
−
2
y
−
z
+
14
0
, mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
−
4
y
−
6
z
−
11...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ( a ) : 2 x − 2 y − z + 14 = 0 , mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x − 4 y − 6 z − 11 = 0 . Mặt phẳng (P)//(a) cắt (S) theo thiết diện là một hình tròn có diện tích 16 π . Khi đó phương trình mặt phẳng (P) là
A. 2 x − 2 y − z + 14 = 0
B. 2 x − 2 y − z + 4 = 0
C. 2 x − 2 y − z + 16 = 0
D. 2 x − 2 y − z − 4 = 0
Trong không gian với trục tạo độ Oxyz, cho mặt phẳng (
α
): 2x - 2y + z -3 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
+
4
y
-
6
z
+
9
0
. Khi đó, phát biểu nào sau đây đúng? A. (
α...
Đọc tiếp
Trong không gian với trục tạo độ Oxyz, cho mặt
phẳng ( α ): 2x - 2y + z -3 = 0 và mặt cầu
(S): x 2 + y 2 + z 2 - 2 x + 4 y - 6 z + 9 = 0 . Khi đó,
phát biểu nào sau đây đúng?
A. ( α ) không cắt (S)
B. ( α ) tiếp xúc với (S)
C. ( α ) cắt (S) theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S)
D. ( α ) cắt (S) theo giao tuyến là một đường tròn có tâm trùng với tâm của (S)
Đáp án C
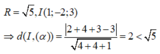
⇒ ( α ) cắt ( β ) theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S)
Đúng 0
Bình luận (0)
Trong không gian với trục tọa độ Oxy, cho mặt phẳng
(
α
)
:
2
x
−
2
y
+
z
−
3
0
và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
−
2
x
+
4
y
−
6
z
+...
Đọc tiếp
Trong không gian với trục tọa độ Oxy, cho mặt phẳng ( α ) : 2 x − 2 y + z − 3 = 0 và mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x + 4 y − 6 z + 9 = 0 . Khi đó, phát biểu nào sau đây đúng?
A. ( α ) không cắt (S).
B. ( α ) tiếp xúc với (S).
C. ( α ) cắt theo giao tuyến là một đường tròn có bán kính nhỏ hơn bán kính của (S).
D. ( α ) cắt (S) theo giao tuyến là một đường tròn có tâm trùng với tâm của (S).
Trong không gian với hệ tọa độ Oxyz mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
−
2
x
+
4
y
−
6
z
−
2
0
. Khi đó (S) có: A...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz mặt cầu (S) có phương trình x 2 + y 2 + z 2 − 2 x + 4 y − 6 z − 2 = 0 . Khi đó (S) có:
A. Tâm I − 2 ; 4 ; − 6 và bán kính R = 58
B. Tâm I 2 ; − 4 ; 6 và bán kính R = 58
C. Tâm I − 1 ; 2 ; − 3 và bán kính R = 4
D. Tâm I 1 ; − 2 ; 3 và bán kính R = 4
Đáp án D
Phương trình mặt cầu có dạng: x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 có tâm I a ; b ; c , bán kính
Đúng 0
Bình luận (0)
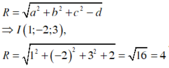
Biết x^2 + y^2 +z^2 + 2x - 4y + 6z = -14. Khi đó x+y+z có giá trị là
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
H24
1 tháng 4 2022 lúc 9:25
Chứng minh:
a. x2 + xy + y2 + 1 > 0 với mọi x, y
b. x2 + 4y2 + z2 - 2x - 6z + 8y + 15 > 0 Với mọi x, y, z
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
x^2+4y^2+z^2-2x-6z+8y+15
=x^2+4y^2+z^2-2x-6z+8y+1+1+4+9
=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1
=(x-1)^2+4(y+1)^2+(z-3^)2+1
Ta thấy:(x−1)^2≥0
4(y+1)^2≥0
(z−3)^ 2≥0
{(x−1)^24(y+1)^2(z−3)^2≥0
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
⇒(x−1)2+4(y+1)2+(z−3)2+1≥0+1=1>0
Đúng 3
Bình luận (1)
\(x^2+xy+y^2+1.=x^2+2.x.\dfrac{y}{2}+\left(\dfrac{y}{2}\right)^2+\dfrac{3}{4}y^2+1.\\ =\left(x+\dfrac{y}{2}\right)^2+\dfrac{3}{4}y^2+1>0\forall x;y\in R.\\ \Rightarrow x^2+xy+y^2+10\forall x;y\in R.\)
Đúng 3
Bình luận (0)
Biết x2 + y2 + z2 + 2x -4y +6z = -14 . Khi đó tổng x+y+z có giá trị là ____
x2 + y2 +z2 + 2x - 4y+6z + 14=0
(x2 + 2x +1) + (y2 - 2.y.2 +22) + (z2 + 2.z.3 +32) =0
(x+1)2 + (y-2)2 +(z+3)2 =0
vì (x+1)2 >= 0; (y-2)2>=0 ; (z+3)2>=0
nên x+1=0 và y-2=0 và z+3=0
x=-1 ; y=2 ; z=-3
vậy x+y+z=-2
Đúng 0
Bình luận (0)
2 nha bn
chuc bn hoc tot
happy new year
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho mặt phẳng (P):2x-2y-z-40 và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
11
0
. Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C) là:
Đọc tiếp
Trong không gian Oxyz cho mặt phẳng (P):2x-2y-z-4=0 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C) là:
