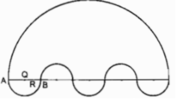
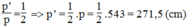Tính chu vi của hình bên biết \(OA=OB=R>0\)
(h.bs.5)
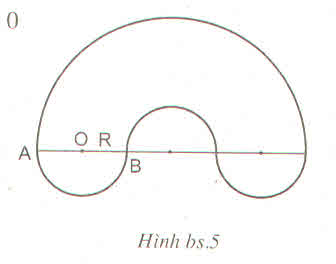
Tính chu vi của hình bên biết OA = OB = R > 0 (h.bs.5).
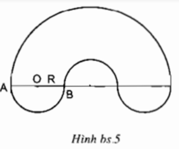
Hình đó gồm một nửa đường tròn bán kính 3R và 3 nửa đường tròn có bán kính R. Do đó, chu vi của hình đã cho là
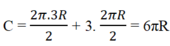
Tính chu vi của hình cánh hoa, biết OA = R (h.bs.6).
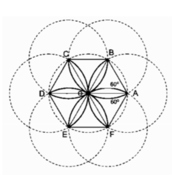
Ta có 12 cung đơn hoặc 6 cung kép tạo nên cánh hoa đó.
Xét một cung kép, chẳng hạn BOF, là cung của một đường tròn tâm A bán kính R với góc ở tâm là 120 ° , nên có độ dài là

Tính diện tích của hình được giới hạn bởi các đường cong, biết OA = OB = R > 0 (h.bs.7).
Hình đó gồm nửa hình tròn bán kính 5R, 3 nửa hình tròn bán kính R và bớt đi 2 nửa hình tròn bán kính R.
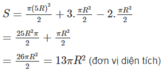
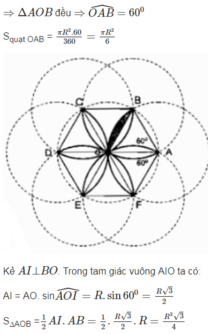
Tính diện tích của hình cánh hoa, biết OA = R (h.bs.8).
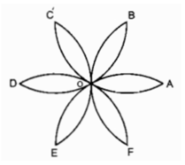
Ta có 12 hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
Xét hình viên phân giới hạn bởi cung BO và dây căng cung đó thì cung BO là cung của đường tròn tâm A bán kính R.
OA = AB = OB = R

Câu 4: Cho ΔABC, điểm O ở bên trong tam giác. Gọi theo thứ tự là trung điểm của OA, OB, OC.
a) Chứng minh rằng ΔABC đồng dạng với ΔMNP.
b) Tính chu vi của ΔMNP biết chu vi của ΔABC bằng 88cm.
Câu 4: Cho ΔABC, điểm O ở bên trong tam giác. Gọi theo thứ tự là trung điểm của OA, OB, OC.
a) Chứng minh rằng ΔABC đồng dạng với ΔMNP.
b) Tính chu vi của ΔMNP biết chu vi của ΔABC bằng 88cm.
Câu 4: Cho ΔABC, điểm O ở bên trong tam giác. Gọi theo thứ tự là trung điểm của OA, OB, OC.
a) Chứng minh rằng ΔABC đồng dạng với ΔMNP.
b) Tính chu vi của ΔMNP biết chu vi của ΔABC bằng 88cm.
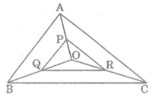
Cho điểm O nằm trong ΔABC. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a. Chứng minh: ΔPQR đồng dạng ΔABC b. Tính chu vi ΔPQR, biết chu vi ΔABC bằng 540 cm.
a. Xét △OAB có:
Q là trung điểm OB, P là trung điểm OA (gt).
\(\Rightarrow\) PQ là đường trung bình của △OAB.
\(\Rightarrow PQ=\dfrac{1}{2}AB\)
\(\Rightarrow\dfrac{PQ}{AB}=\dfrac{\dfrac{1}{2}AB}{AB}=\dfrac{1}{2}\)
-Tương tự: \(\dfrac{QR}{BC}=\dfrac{1}{2};\dfrac{PR}{AC}=\dfrac{1}{2}\)
-Xét △PQR và △ABC có:
\(\dfrac{PQ}{AB}=\dfrac{QR}{BC}=\dfrac{PR}{AC}\left(=\dfrac{1}{2}\right)\)
\(\Rightarrow\)△PQR ∼ △ABC (c-c-c).
b. Ta có: △PQR ∼ △ABC (cmt).
\(\Rightarrow\dfrac{S_{PQR}}{S_{ABC}}=\left(\dfrac{PQ}{AB}\right)^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
\(\Rightarrow S_{PQR}=\dfrac{1}{2}S_{ABC}=\dfrac{1}{2}.540=270\left(cm^2\right)\)
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm.
Gọi p’ là chu vi tam giác PQR.
Tacó: 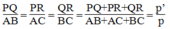
Vậy: