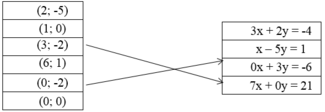
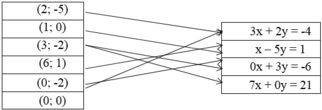
Cho các cặp số và các phương trình sau.
| \(\left(2;-5\right)\) |
| \(\left(1;0\right)\) |
| \(\left(3;-2\right)\) |
| \(\left(6;1\right)\) |
| \(\left(0;-2\right)\) |
| \(\left(0;0\right)\) |
Hãy chỉ rõ mỗi cặp số là nghiệm của những phương trình nào sau đây :
1) \(3x+2y=-4\);
2) \(x-5y=1\);
3) \(0x+3y=-6\);
4) \(7x+0y=21\).