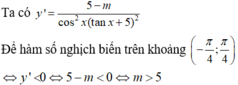Cho tanx=3tany tìm giá trị của x-y
NT
Những câu hỏi liên quan
cho tanx=3tany, 0<x,y<π/2.
Chứng minh x-y≤π/6
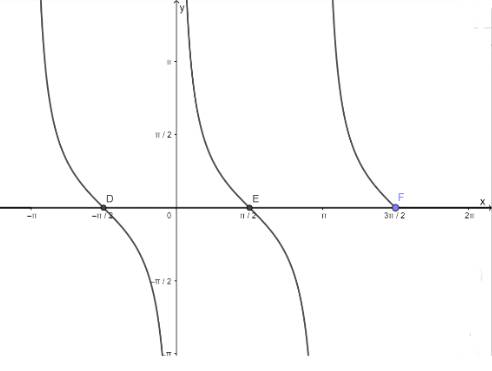
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
a) Hàm số y = tanx nhận giá trị bằng – 1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
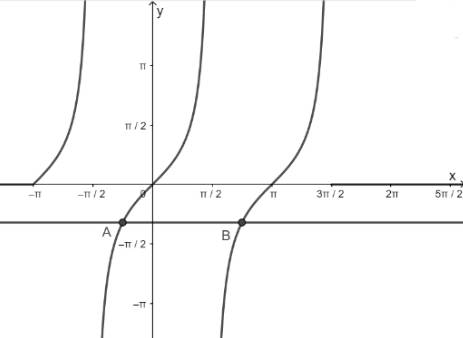
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
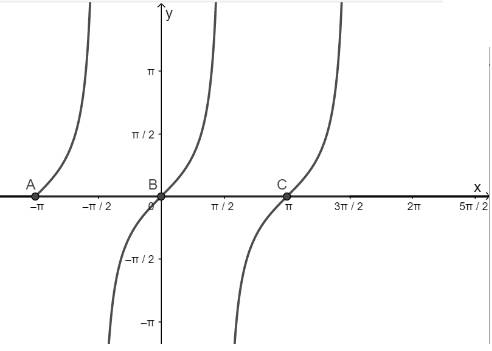
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
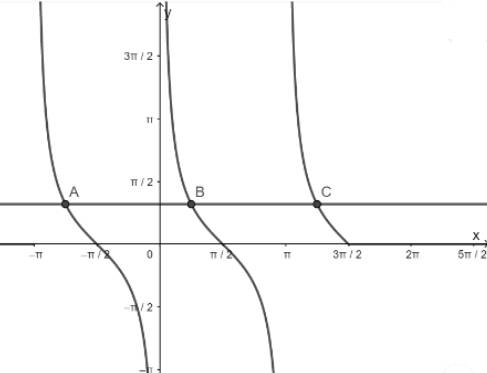
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y tanx, x ∈ (
-
π
3
;
π
6
) A:
max
y
3
3
;
min
y
1
2
B: max y 3...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y = tanx, x ∈ ( - π 3 ; π 6 )
A: max y = 3 3 ; min y = 1 2
B: max y = 3; min y = -1
C: max y = 1; min y = -![]()
D: Đáp án khác
Tìm giá trị nhỏ nhất của hàm số sau y= tan2 x+cot2 x + 3.( tanx + cot x) – 1
A. - 5
B. - 3
C . -2
D. – 4
Ta có:
y = tan2 x+ cot2 x+ 3. (tanx+ cotx) – 1
= ( tanx +cotx)2 +3. ( tanx +cot x) – 3
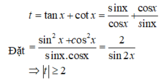
Suy ra y= t2 + 3t – 3 = f (t)
Bảng biến thiên
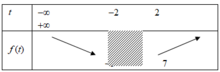
Vậy min y= - 5 đạt được khi t = - 2
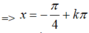
Không tồn tại max y
Đáp án A
Đúng 0
Bình luận (0)
Cho
tan
x
-
tan
y
10
v
à
c
o
t
x
-
c
o
t
y
5
. Giá trị của
tan
x
-
y
là A. 10 B. -10 C.
-
1
10
...
Đọc tiếp
Cho tan x - tan y = 10 v à c o t x - c o t y = 5 . Giá trị của tan x - y là
A. 10
B. -10
C. - 1 10
D. 1 10
Chọn B.

Kết hợp với tan x - tan y = 10 thì ta được tan x . tan y = - 2 .
Do đó
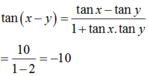
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m sao cho hàm số
y
tan
x
+
m
tan
x
+
5
nghịch biến trên
-
π
4
;
π
4
A. 1 m 5 ...
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho hàm số y = tan x + m tan x + 5 nghịch biến trên - π 4 ; π 4
A. 1 < m < 5
B. m ≥ 5
C. m < -1 hoặc m > 5
D. m > 5
Cho hàm số
y
f
(
x
)
tan
x
+
cot
x
. Giá trị
f
π
4
bằng A.
2
B. 0 C.
2
2
D.1
Đọc tiếp
Cho hàm số y = f ( x ) = tan x + cot x . Giá trị f ' π 4 bằng
A. 2
B. 0
C. 2 2
D.1
Chọn B
y ' = 1 2 tan x + cot x . ( tan x + cot x ) ' = 1 2 tan x + cot x . 1 cos 2 x − 1 sin 2 x ⇒ y ' π 4 = 1 2 1 + 1 . 1 1 2 − 1 1 2 = 0
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
sin
x
+
cos
x
+
tan
x
+
c
o
t
x
+
1...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = sin x + cos x + tan x + c o t x + 1 sin x + 1 cos x
A. 2 2 - 1
B. 2 + 1
C. 2 2 + 1
D. 2 - 1
Đáp án A
Phương pháp: Đặt sinx = a, cosx = b
Cách giải: Đặt sinx = a, cosx = b ta có a2 + b2 = 1
Khi đó 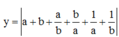
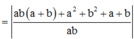
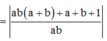
Đặt 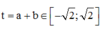
![]()
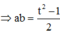
khi đó ta có : 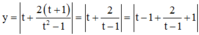
Nếu 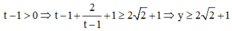
Nếu ![]()
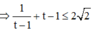
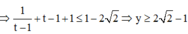
Vậy ![]()
Dấu bằng xảy ra ![]()
![]()
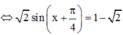
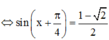
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
tan
x
−
2
tan
x
−
m
đồng biến trên khoảng
−
π
4
;
0
. A.
−
1
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = tan x − 2 tan x − m đồng biến trên khoảng − π 4 ; 0 .
A. − 1 ≤ m < 2
B. m < 2
C. m ≥ 2
D. m ≤ − 1 0 ≤ m < 2
Đáp án D
Chú ý bằng điều kiện hàm hợp:
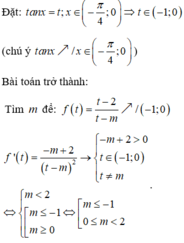
Đúng 0
Bình luận (0)