Tìm tất cả bộ ba số nguyên tố (m, n, p) sao cho mnp < mn + np + pm.
TN
Những câu hỏi liên quan
Tìm tất cả các số nguyên tố m,n sao cho 7m n và mn 11 là số nguyên tố
Tìm tất cả các số nguyên tố m,n sao cho 7m+n và mn +11 là số nguyên tố
https://olm.vn/hoi-dap/detail/1334571579.html
Tìm tất cả các số nguyên tố m,n sao cho 7m+n và mn+11 cũng là số nguyên tố
Để 7m+n là số nguyên tố, mà 7m+n>2 thì m,n không cùng tính chẵn lẻ
=> m,n có một số bằng 2
+ Nếu m=2. Ta có:\(\hept{\begin{cases}n+14\\2n+11\end{cases}}\)đều là số nguyên tố
Thấy n=3 thỏa. Xét n=3k+1
=>n+14=3k+15=3(k+5) là hợp số.
Tương tự với 2n+11
+ Nếu n=2.
Hoàn toàn tương tự trường hợp trên.
Kết quả: (m;n)=(2;3),(3;2) thỏa mãn đề bài.
Bạn có thể làm rõ ràng hơn không ? Mình đọc hơi khó hiểu.
Tương tự với 2n + 11 là như thế nào?
Nếu n=2 Xét n=2k+1
=> 2n+11=2k+12 = 2 (k+12) là hợp số
tìm tất cả các số nguyên tố m,n sao cho 7m + n và mn + 11 cũng là số nguyên tố
Tìm tất cả các bộ ba số nguyên tố liên tiếp sao cho tổng các bình phương của ba số này cũng là số nguyên tố?
Tìm tất cả bộ ba các số nguyên tố liên tiếp sao cho tổng bình phương của 3 số đó cũng là số nguyên tố.
Gọi 3 số nguyên tố liên tiếp cần tìm là p, q, r.
Ta có p2 + q2 + r2 = A là số nguyên tố.
Giả sử p < q < r
Do p, q, r là các số nguyên tố nên A = p2 + q2 + r2 > 3 nên
Nếu p, q, r đều không chia hết cho 3 khi đó p2 ; q2 ;r2 khi chia cho 3 dư 1 hoặc dư 2.
=> A chia hết cho hết cho 3 mà A > 3 nên A là hợp số trái với giả thiết (loại)
Vậy p chia hết cho 3, vì p nguyên tố nên p = 3 \(\Rightarrow\) q = 5 ; r = 7
Khi đó 32 + 52 + 72 = 83 là số nguyên tố
Vậy 3 số nguyên tố cần tìm chỉ có 3 ; 5 ; 7 thỏa mãn.
Đúng 0
Bình luận (0)
Đinh Tuấn Việt nhầm rồi:
Sửa lại: p; q;r là số nguyên tố > 3 => chúng có dạng 3k + 1 hoặc 3k + 2
=> p2; q2; r2 chia cho 3 đều dư 1
=> p2 + q2+ r2 chia hết cho 3 => A chia hết cho 3
.....................
Đúng 0
Bình luận (0)
đinh tuấn việt nhầm rồi ; 1 SNT ko chia hết cho 3 khi bình phương lên chia 3 dư 1 nên mới suy ra được là A chia hết cho 3
Đúng 0
Bình luận (0)
Tìm Tìm tất cả các bộ ba số nguyên tố a, b, c sao cho abc < ab + bc + ca
Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
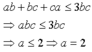
( Vì a là số nguyên tố )
Với a = 2 ta có
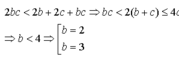
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .
Đúng 0
Bình luận (0)
Có bao nhiêu bộ ba số nguyên theo thứ tự (m, n, p) tồn tại sao cho mn = p, np = m và mp = n?
Ta có: \(\hept{\begin{cases}mn=p\\np=m\\mp=n\end{cases}}\)Nhân theo vế: \(\left(mnp\right)^2=mnp\Leftrightarrow mnp\left(mnp-1\right)=0\Leftrightarrow\orbr{\begin{cases}mnp=0\\mnp=1\end{cases}}\)
Khi mnp=0,với m hoặc n hoặc p=0 thì ta luôn tìm được 2 số còn lại cũng bằng 0,hay \(m=n=p=0\)
Khi mnp=1,kết hợp với m;n;p nguyên ,ta tim được \(m=n=p=1\)hoặc \(m;n;p\)là hoán vị \(-1;-1;1\)
Đúng 0
Bình luận (0)
Cho A = a + b + c + m + n + p ; B = ab + bc + ca - mn - np - pm ; C = abc + mnp . Biết a, b, c, m , n , p là các số nguyên dương và Cả B và C đều chia hết cho A. CMR A là 1 hợp số


