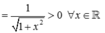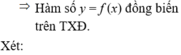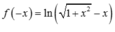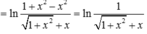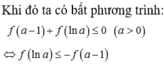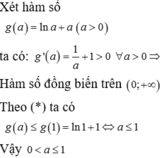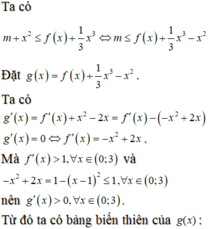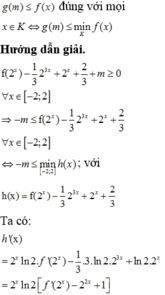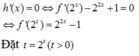cho hàm số y=f(x)=x2. Tìm m để bất phương trình f(x-3)+5-m>0 cố tập nghiệm là R
LK
Những câu hỏi liên quan
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.
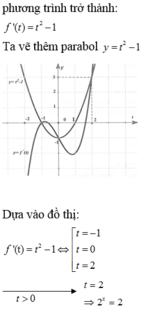
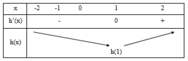
Với thì PT có nghiệm (chọn)
Với thì là đa thức bậc 2 ẩn
có nghiệm khi mà
Tóm lại để có nghiệm thì
Cho hàm số
y
f
(
x
)
ln
(
1
+
x
2
+
x
)
. Tập nghiệm của bất phương trình
f
(
a
-
1
)
+
f
(
ln
a
)
≤
0
là:
Đọc tiếp
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Bảng biến thiên của hàm số yf(x) như hình dướiTìm m để bất phương trình
m
+
x
2
≤
f
(
x
)
+
1
3
x
3
nghiệm đúng với mọi
x
∈
0
;
3...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Bảng biến thiên của hàm số y=f'(x) như hình dưới
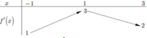
Tìm m để bất phương trình m + x 2 ≤ f ( x ) + 1 3 x 3 nghiệm đúng với mọi x ∈ 0 ; 3
A. m<f(0)
B. m ≤ f ( 0 ) .
C. m ≤ f ( 3 )
D. m< f ( 1 ) - 2 3
Cho hàm số
f
(
x
)
l
n
(
x
2
-
2
x
+
3
)
. Tập nghiệm của bất phương trình f(x)0 là A.
(
2
;
+
∞
)
. B.
(
-
1
;
+
∞
)
. C.
(
-
2
;
+
∞
)...
Đọc tiếp
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Cho hàm số yf(x) có đạo hàm liên tục trên R, đồ thị hàm số yf(x) như hình vẽ bên dưới. Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R, đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
đúng với mọi
x
∈
-
2
;
2
![]()
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Đồ thị của hàm số yf(x) như hình dưới Tìm m để bất phương trình
m
+
x
2
+
4
≥
2
f
x
+
1
-
2
x
nghiệm đúng với mọi
x
∈...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị của hàm số y=f'(x) như hình dưới
Tìm m để bất phương trình m + x 2 + 4 ≥ 2 f x + 1 - 2 x nghiệm đúng với mọi x ∈ - 4 ; 2
A. m ≥ 2 f ( 0 ) - 1
B. m ≥ 2 f ( - 3 ) - 4
C. m ≥ 2 f ( 3 ) - 16
D. m ≥ 2 f ( 1 ) - 4
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Bảng biến thiên của hàm số yf(x) như hình dưới Tìm m để bất phương trình
m
+
2
sin
x
≤
f
(
x
)
nghiệm đúng với mọi
x
∈
0
;
+
∞
. A. m f(0) +1 B. m f(1) C. m f(0) D. m f(0) -1
Đọc tiếp
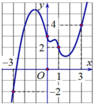
Cho hàm số y=f(x) có đạo hàm trên ℝ . Bảng biến thiên của hàm số y=f'(x) như hình dưới
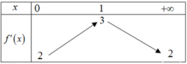
Tìm m để bất phương trình m + 2 sin x ≤ f ( x ) nghiệm đúng với mọi x ∈ 0 ; + ∞ .
A. m < f(0) +1
B. m < f(1)
C. m < f(0)
D. m < f(0) -1
Đáp án C
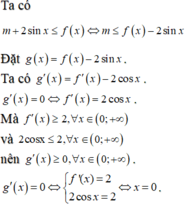
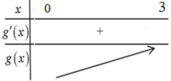
Từ đó ta có bảng biến thiên của g(x):
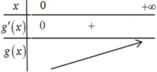

Đúng 0
Bình luận (0)
Cho hàm số f ( x ) = 1 3 x 3 - x 2 + 2 x - 2009 . Tập nghiệm của bất phương trình f'(x) ≤ 0 là:
A. ∅
B. [-2;2]
C. 0 ; + ∞
D. R
Chọn A
- Ta có:
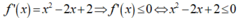
- Suy ra bất phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ. Biết trên
(
-
∞
;
-
3
)
∪
(
2
;
+
∞
)
t
h
ì
f
(
x
)
0
. Số nghiệm nguyên thuộc (-10; 10) của bất phương trình
[
f
(
x
)...
Đọc tiếp
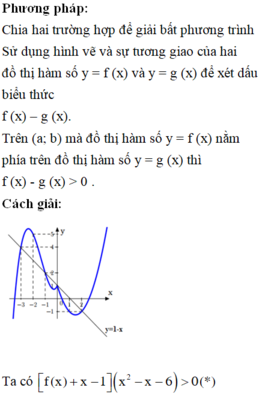
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
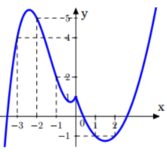
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7