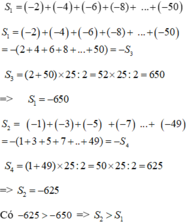So sánh : S1 = 1+2+2^2+2^3+...............+262014 và S2 = 2^2015-1
LC
Những câu hỏi liên quan
So sánh :
S1 = 1+2+2^2+2^3+...............+262014
và
S2 = 2^2015-1
So sánh
S1 = 1 + 2 +2^2 + 2^3 +..............+2^2014
với
S2 = 2^2015 - 1
So sánh
S
1
và
S
2
S
1
−
2
+
−
4
+
−
6
+
(
−
8
)
+
...
+
−
50...
Đọc tiếp
So sánh S 1 và S 2
S 1 = − 2 + − 4 + − 6 + ( − 8 ) + ... + − 50 S 2 = − 1 + − 3 + − 5 + − 7 ... + − 49
So sánh s1 và s2
s1:2+4+6+...+5000
s2:2.2.5.5.5.5.2051
Thu gọn các biểu thức:
S1=4+2^2+2^3+.....+2^2015
S2=3+3^2+3^3+.....+3^2015
S1=1+(-2)+3+(-4)+...+(-2014)+2015
S2=1+(-3)+5+(-7)+...+2013+(-2015)
Ai giúp mình với!!!!!!!!!!!!Mik cần vô cùng gấp lun.Help me.Thanks:33
Tính tổng:S1=1+(-2)+3+(-4)+...+2015+(-2016). S2=(-2)+(-4)+(-6)+...+(-2020).S3=1+(-3)+5+(-7)+...2013+(-2015) mình đang cần gấp các bạn giúp mình nhé!
Xem chi tiết
Tính tổng:
S1=1+(-2)+3+(-4)+...+2015+(-2016).
S1=[1+(-2)]+[3+(-4)]+...+[2015+(-2016)]
S1=-1+(-1)+...+(-1) ( có 1008 số -1 )
S1=-1.1008
S1=-1008
S3=1+(-3)+5+(-7)+...2013+(-2015)
S3=[1+(-3)]+[5+(-7)]+...+[2013+(-2015)]
S3=-2+(-2)+...+(-2) ( có 1008 số -2)
S3=-2016
cho mình cả s2 bạn ơi,thank bạn
Thu gọn biểu thức
S1=4+4 mũ 2+2 mũ 3+2 mũ 4+....+2 mũ 2015
S2=3+3 mũ 2+3 mũ 3+....+3 mũ 2015
S3=3-3 mũ 3+3 mũ 5-.....+3 mũ 2013 - 3 mũ 2015+3 mũ 2017
S4=2 mũ n -1+2.2 mũ n -2+3.2 mũ n-3+....+(n-1).2+n
1) So sánh 20162015 và 20152016
2) So sánh 22014 và 5891
3) So sánh (20152016+20162016)2015 và (20152015+20162015)2016
Ta có:
\(\left(2015^{2015}+2016^{2015}\right)^{2016}=\left(2015^{2015}+2016^{2015}\right)^{2015}.\left(2015^{2015}+2016^{2015}\right)\)
\(>\left(2015^{2015}+2016^{2015}\right)^{2015}.2016^{2015}=\left[\left(2015^{2015}+2016^{2015}\right)2016\right]^{2015}\)
\(>\left(2015^{2015}.2015+2016^{2015}.2016\right)^{2015}=\left(2015^{2016}+2016^{2016}\right)^{2015}\)
Vậy \(\left(2015^{2015}+2016^{2015}\right)^{2016}>\left(2015^{2016}+2016^{2016}\right)^{2015}\)
Đúng 0
Bình luận (0)
1. Ta sẽ chứng minh \(2015^{2016}>2016^{2015}\)
\(\Leftrightarrow2016^{2015}-2015^{2016}< 0\Leftrightarrow2016^{2016}-2016.2015^{2016}< 0\)
\(\Leftrightarrow2016.2016^{2016}-2015.2016^{2016}-2016.2015^{2016}< 0\)
\(\Leftrightarrow2016\left(2016^{2016}-2015^{2016}\right)< 2015.2016^{2016}\)
\(\Leftrightarrow2016\left(2016^{2015}+2016^{2014}.2015+...+2015^{2015}\right)< 2015.2016^{2016}\)
\(\Leftrightarrow2016^{2015}.2015+...+2016.2015^{2015}< 2014.2016^{2016}\)
\(\Leftrightarrow2016^{2014}.2015+2016^{2013}.2015^2+...+2015^{2015}< 2014.2016^{2015}\)
\(\Leftrightarrow2015^{2015}< \left(2016^{2015}-2015.2016^{2014}\right)+\left(2016^{2015}-2015^2.2016^{2013}\right)\)
\(+...+\left(2016^{2015}-2015^{2014}.2016\right)\)
\(\Leftrightarrow2015^{2015}< 2014.2016^{2014}+2013.2016^{2014}.2015+...+2016.2015^{2013}\)
Lại có \(2015^{2015}=2014.2015^{2014}+2015^{2014}< 2014.2016^{2014}+2015^{2014}\)
Mà \(2015^{2014}< 2013.2016^{2014}.2015\)
nên \(2015^{2014}< 2014.2016^{2014}+2013.2016^{2014}.2015+...+2016.2015^{2013}\)
Vậy \(2015^{2016}>2016^{2015}.\)
Đúng 0
Bình luận (0)