hàm số y= ax2 +bx+c =0 khi x=1. giả sử b khác 0 khi đó ta có \(\dfrac{a+c}{b}=\)
NH
Những câu hỏi liên quan
hàm số y=ax^2+bx+c bằng 0 khi x=1. giả sử b khác 0, khi đó ta có a+c/b=
HÀM số y=ax^2+bx+c bằng 0 khi x=1.Giả sử b khác 0 khi đó ta có a+c/b bằng
hàm số y=ax^2+bx+c bằng 0 khi x=1. giả sử b khác 0, khi đó ta cóa+c/b=
x=1 => \(x=1\Rightarrow y=ax^2+bx+c=a.1+b.1+c=a+b+c=0\)
Giả sử b khác 0 => a + c = - b để thỏa mãn cho a+b+c=0 => \(\frac{a+c}{b}=\frac{-b}{b}=-1\)
Đúng 0
Bình luận (0)
Hàm số \(y=ax^2+bx+c\)
bắng 0 khi x=1.
Giả sử b khác 0, khi đó ta có \(\frac{a+c}{b}=........\)
Từ \(x=1\Rightarrow a+b+c=0\)
\(\Rightarrow a+c=-b\)
\(\Rightarrow\frac{a+c}{-b}=1\Rightarrow\frac{a+c}{b}=-1\)
Đúng 0
Bình luận (0)
\(y=ax^2+bx+c=a1^2+b1+c=a+b+\)\(c=0\)
b khác 0 suy ra a và c trái dấu
a và c trái dấu suy ra a+c =0
khi đó ta có \(\frac{a+c}{b}=0\)
Đúng 0
Bình luận (0)
hàm số y=ax^2+bx+c bằng 0 khi x=1. giả sử b khác 0, khi đó ta có a+c/b= (đang cần gấp kết quả, ai xong trc tick ngay)
Tìm a, b, c sao cho hàm số
y
x
3
+
a
x
2
+
b
x
+
c
có giá trị bằng 0 khi x 1 và đạt cực trị khi bằng 0 khi x -1 . A.
a
-
1
;
b
1
;
c
1
B.
a...
Đọc tiếp
Tìm a, b, c sao cho hàm số y = x 3 + a x 2 + b x + c có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .
A. a = - 1 ; b = 1 ; c = 1
B. a = - 1 2 ; b = - 1 ; c = - 1 2
C. a = 1 ; b = - 1 ; c = - 1
D. a = 1 2 ; b = - 1 ; c = 1 2
Sử dụng giả thiết và điều kiện cần của cực trị ta có
y(1) = 0; y'(-1) = 0; y(-1) = 0
Trong đó , y ' = 3 x 2 + 2 a x + b
Từ đó suy ra:
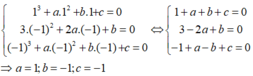
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành y = x 3 + x 2 - x - 1
Ta có y ' = 3 x 2 + 2 x - 1 , y ' ' = 6 x + 2 . V ì y ' ' = ( - 1 ) = - 4 < 0 nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Hàm số y=ax^2 +bx+c bằng 0 khi x=1Giả sử bkhác 0,khi đó ta có a+c/b = ?
Cho hàm số
f
x
a
x
2
+
b
x
+
c
khi
x
≥
0...
Đọc tiếp
Cho hàm số f x = a x 2 + b x + c khi x ≥ 0 a x - b - 1 khi x < 0 . Khi hàm số f(x) có đạo hàm tại x 0 = 0 . Tính giá trị biểu thức T = a + 2b
A. -4
B. 0
C. -6
D. 4
cho hàm số y = ax^2 + bx + c(a khác 0). tìm a, b, c biết hàm số đó có gtln = 5 khi x = -2 và đồ thị đi qua M(1;-1)
\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...
Đúng 2
Bình luận (0)


