em hãy chứng minh, trong tam giác ABC có : CA+CB>AB và BA+BC>CA
DS
Những câu hỏi liên quan
Em hãy chứng minh ,tam giác ABC có CA+CB>AB và BA +BC >CA
Áp dụng bất đẳng thức trong tam giác ABC:
=> CA+CB>AB;BA+BC>CA
Đúng 0
Bình luận (0)
Trong tam giác ABC kẻ AD sao cho AD _|_ BC ( D thuộc BC )
Xét tam giác ADC vuông tại D có :
Theo định lý Py-ta-go : AD2+DC2=AC2
=> DC > AC (1)
Xét tam giác ADB vuông tại D có :
Theo định lý Py-ta-go : AD2+DB2=AB2
=> DB<AB (2)
Từ (1) và (2) <=> DC+DB<AC+AB hay AB+AC>BC
Cho tam giác ABC. Trên tia đối của AB lấy điểm D sao cho AC = AD
Khi đó AB + AC = AB + AD = BD, còn ACD là tam giác cân, nên góc ACD = góc ADC, tức là góc BDC = góc ACD
Mặt khác, do tia CA nằm giữa CB và CD nên góc BCD > góc DCA
Khi đó, trong tam giác BCD có: góc BCD > góc BDC nên BD > BC hay AB + AC > BC
Tương tự, em hãy chứng minh, trong tam giác ABC có: CA + CB > AB và BA + BC > CA
em hãy chứng minh trong tam giác ABC có CA+CB>AB và BA+BC>CA
Trong tam giác ABC kẻ AD sao cho AD _|_ BC ( D thuộc BC )
Xét tam giác ADC vuông tại D có :
Theo định lý Py-ta-go : AD2+DC2=AC2
=> DC > AC (1)
Xét tam giác ADB vuông tại D có :
Theo định lý Py-ta-go : AD2+DB2=AB2
=> DB<AB (2)
Từ (1) và (2) <=> DC+DB<AC+AB hay AB+AC>BC
Đúng 0
Bình luận (2)
Kẻ AH ⊥ BC
Xét ΔABH vuông tại H có:
∠AHB vuông, nên AB là cạnh lớn nhất
do đó: AB>BH (1)
Xét ΔACH vuông tại H có:
∠AHC vuông, nên AC là cạnh nhất
do đó: AC>CH (2)
Từ (1),(2) ta suy ra: AB+AC>BH+CH
Mà BH +CH=BC
nên AB+AC>BC
Giả sử BC là cạnh lớn nhất, ta suy ra:
AB<BC
AC<BC
Vậy AC+BC>AB; AB+BC>AC
Đúng 0
Bình luận (0)
Cho tam giác ABC. Trên tia BC lấy BA' =2BC, trên tia CA lấy CB' =2CA; trên tia AB lấy AC' = 2AB. Chứng minh hai tam giác ABC và A'B'C' có cùng trọng tâm
cho tam giác abc. o nằm trong tam giác. qua o kẻ đường thẳng song song với bc cắt ab, ac ở m, n, đường thẳng song song với ca cắt ba, bc ở f, k, đường thẳng song song với ab cắt ca, cb ở d,e. chứng minh af/ab + be/bc + cn/ca = 1
Cho tam giác ABC điểm O nằm trong tam giác, tia BO cắt cạnh AC tại Ia) So sánh OA và IA + IO, từ đó suy ra OA + OB IA + IB;b) Chứng minh OA + OB CA + CB.c) Chứng minh
A
B
+
B
C
+
C
A
2
O
A
+
O
B
+
O...
Đọc tiếp
Cho tam giác ABC điểm O nằm trong tam giác, tia BO cắt cạnh AC tại I
a) So sánh OA và IA + IO, từ đó suy ra OA + OB < IA + IB;
b) Chứng minh OA + OB < CA + CB.
c) Chứng minh A B + B C + C A 2 < O A + O B + O C < A B + B C + C A
Chứng minh trong một tam giác ABC có: CA + CB > AB và BA + BC >CA
Trong 1 tam giác, tổng 2 cạnh bất kì luôn lớn hơn cạnh còn lại nên CA + CB> AB và BA + BC> CA
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm O nằm trong tam giác, tia BO cắt cạnh AC tại I. a) So sánh OA và IA + IO, từ đó suy ra OA + OB < IA + IB; b) Chứng minh: OA + OB < CA + CB; c) Chứng minh: (AB+AC+BC) /2 < OA + OB + OC < AB + BC + CA
Cho tam giác ABC, ba điểm M, N, P lần lượt thuộc BC, CA, AB sao cho BM/BC = CN/CA = AP/AB và BM/BC < 1/2. Chứng minh tam giác ABC và MNP có cùng trọng tâm



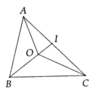
 tham khảo nha
tham khảo nha