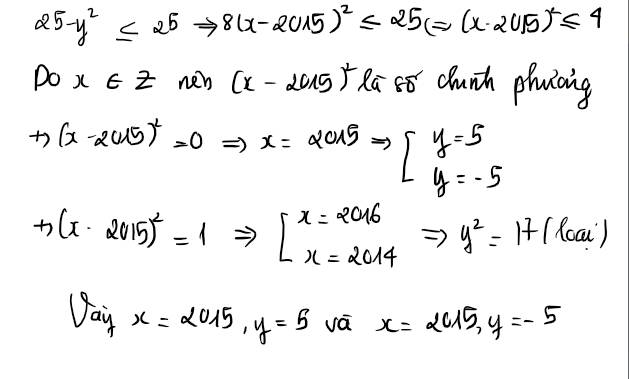Ta có: VP\(\ge0\)=> VT \(\ge0\)

Ta có: VT\(\le25\)=> VP\(\le25\)\(\Leftrightarrow8\left(x-2016\right)^2\le25\Leftrightarrow\left(x-2016\right)^2\le\frac{25}{8}< 4\)

Do \(x\in N\)=> \(\left(x-2016\right)^2=1\Leftrightarrow x=2017\)hoặc \(\left(x-2016\right)^2=0\Leftrightarrow x=2016\)

Khi đó: \(25-y^2=8\Leftrightarrow y^2=17\)(vô nghiệm y tự nhiên)

hoặc \(25-y^2=0\Leftrightarrow y^2=25\Leftrightarrow y=5\)

Vậy x=2016, y=5

Đề thiếu nhé,

=0 nữa

Bạn thêm điều kiện x,y,z lớn hơn 0 nhé :)

Từ giả thiết ta suy ra : \(a^2=b+4032\Rightarrow\left(x+y+z\right)^2=x^2+y^2+z^2+4032\)

\(\Rightarrow xy+yz+zx=2016\)thay vào :

\(x\sqrt{\frac{\left(2016+y^2\right)\left(2016+z^2\right)}{2016+x^2}}=x\sqrt{\frac{\left(y^2+xy+yz+zx\right)\left(z^2+xy+yz+zx\right)}{x^2+xy+yz+zx}}\)

\(=x\sqrt{\frac{\left(x+y\right)\left(y+z\right)\left(z+y\right)\left(z+x\right)}{\left(x+y\right)\left(x+z\right)}}=x\sqrt{\left(y+z\right)^2}=x\left|y+z\right|=xy+xz\)vì x,y,z > 0

Tương tự : \(y\sqrt{\frac{\left(2016+z^2\right)\left(2016+x^2\right)}{2016+y^2}}=xy+zy\)

\(z\sqrt{\frac{\left(2016+x^2\right)\left(2016+y^2\right)}{2016+z^2}}=zx+zy\)

Suy ra \(P=2\left(xy+yz+zx\right)=2.2016=4032\)

Mik đoán đại thôi sai cũng đừng trách mik nha:

x = 2014

y = 2016

bn ơi câu a có sai đề k

a) Sai đề

b) \(25-y^2=8\left(x-2016\right)^2\)

\(\Leftrightarrow5^2-y^2=8\left(x-2016\right)^2\)

\(\Leftrightarrow\left(5^2-y^2\right)-8\left(x-2016\right)^2=0\)

Mà \(8\left(x-2016\right)^2\ge0\Rightarrow5^2-y^2\ge8\left(x-2016\right)^2\ge0\)

\(\Rightarrow\left(5^2-y^2\right)-8\left(x-2016\right)^2\ge0\)

Do theo đề bài thì vế phải bằng 0 nên: \(\hept{\begin{cases}5^2-y^2=0\\8\left(x-2016\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=5\\x=2016\end{cases}}\)