tìm các pt đường thẳng đi qua cực đại và cực tiểu của đồ thị hàm số y = -x3 + 3x2 -2
HD
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số a để hàm số
y
x
3
+
3
3
ax
có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số đi qua gốc tọa độ A. a 0 B. a -1 C. -1 a 0 D. a 0
Đọc tiếp
Tìm tất cả các giá trị của tham số a để hàm số y = x 3 + 3 3 ax có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số đi qua gốc tọa độ
A. a < 0
B. a < -1
C. -1 < a < 0
D. a > 0
Tìm tất cả các giá trị của tham số a để hàm số y = x 3 + 3 3 a x có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số đi qua gốc tọa độ
A. a < -1
B. a < 0
C. -1 < a < 0
D. a > 0
Đáp án B
Ta có y ' = 3 x 2 + 3 3 a
Hàm sổ có cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇔ a < 0 .
Hàm số là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ, do đó đường thẳng nối cực đại và cực tiểu của đồ thị hàm số luôn đi qua gốc tọa độ.
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
3
-
3
x
2
-
m
x
+
2
có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình:
y...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 - 3 x 2 - m x + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: y = x - 1 ( d )
A. m = 0
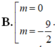
C. m = 2
D. m = - 9 2
Chọn A
[Phương pháp trắc nghiệm]
y ' = 3 x 2 - 6 x - m
Hàm số có 2 cực trị m > -3 , gọi x 1 , x 2 là hai nghiệm của phương trình y ' = 0 ,
ta có: x 1 + x 2 = 2
Bấm máy tính
![]()
![]()
![]()
Hai điểm cực trị của đồ thị hàm số là
![]()
![]()
Gọi I là trung điểm của AB
⇒ I ( 1 ; - m )
Đường thẳng đi qua hai điểm cực trị là
![]()
Yêu cầu bài toán

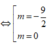
Kết hợp với điều kiện thì m = 0
Đúng 0
Bình luận (0)
Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số
y
x
3
+
3
m
x
2
−
3
x
A.
y
m
x
+
3
m
−
1
B.
y
2
m
3...
Đọc tiếp
Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số y = x 3 + 3 m x 2 − 3 x
A. y = m x + 3 m − 1
B. y = 2 m 3 − 2 x
C. y = − 2 m + 1 x + m
D. y = − 2 x + 2 m
Đáp án B
Phương pháp:
- Gọi là một điểm cực trị của hàm số y = f x , khi đó y ' x 0 = 0 y 0 = x 0 3 + 3 m x 0 2 − 3 x 0
- Từ hệ trên ta tìm được phương trình đường thẳng đi qua x 0 ; y 0 .
Cách giải:
Có: y x = x 3 + 3 m x 2 − 3 x ⇒ y ' x = 3 x 2 + 6 m x − 3
Phương trình đường thẳng d đi qua 2 cực trị của (C) nên x 0 ; y 0 ∈ d thỏa mãn:
y ' x 0 = 0 y 0 = x 0 3 + 3 m x 0 2 − 3 x 0 ⇔ 3 x 0 2 − 6 m x − 3 = 0 y 0 = x 0 x 0 2 + 2 m x 0 − 3 x 0 + m x 0 2
x 0 2 + 2 m x 0 = 1 y 0 = − 2 x 0 + m x 0 2 ⇔ x 0 2 = − 2 m x 0 + 1 y 0 = − 2 x 0 + m − 2 m x 0 + 1
⇒ y 0 = − 2 m 2 + 1 x 0 + m
Chú ý khi giải:
Các em cũng có thể giải bài toán bằng cách khác:
- Tính y'.
- Thực hiện phép chia y cho y' ta sẽ tìm được đa thức dư là kết quả bài toán.
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
3
+
m
x
2
+
7
x
+
3
có đường thẳng đi qua điểm cực đại và điểm cực tiểu vuông góc với đường thẳng có phương trình :
y...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 + m x 2 + 7 x + 3 có đường thẳng đi qua điểm cực đại và điểm cực tiểu vuông góc với đường thẳng có phương trình : y = 3 x ( d )
A. m = ± 45 2
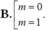
C. m = 2
D. m = ± 47 2
Chọn A
[Phương pháp trắc nghiệm]
y ' = 3 x 2 + 2 m x + 7
![]()
Bấm máy tính
![]()
![]()
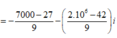
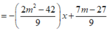
Đường thẳng đi qua 2 điểm cực trị là

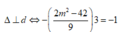
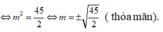
Đúng 0
Bình luận (0)
Đường thẳng nối hai điểm cực đại và cực tiểu của đồ thị hàm số y = x 3 − 3 x + m đi qua điểm M(2;-1) khi m bằng
A. 2
B. -2
C. -3
D. 3
Điểm M ( 3 ; - 1 ) thuộc đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số y = x 3 - x + m khi m bằng
A. 2
B. 1
C. -1
D. 0
Đáp án là B.
• Ta có y , = 3 x 2 - 1 ; Thực hiện phép chia y cho y , ta được: y = 1 3 x ( 3 x 2 - 1 ) - 2 3 x + m
Suy ra phương trình đường thẳng đi qua 2 điểm cực đại,cực tiểu là y = - 2 3 x + m
• Thay M(3;-1) M ( 3 ; - 1 ) ⇒ - 1 = - 2 3 3 + m ⇒ - 1 = - 2 + m ⇒ m = 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y x3- 3mx2+ 4m3 có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng x- y0. A.
m
2
2
B.
m
-
2
2
C. m0 hoặc
m
2
2
D.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y= x3- 3mx2+ 4m3 có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng x- y=0.
A. m = 2 2
B. m = - 2 2
C. m=0 hoặc m = 2 2
D. m = ± 2 2
+ Đạo hàm : y’ = 3x2- 6mx
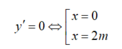
Để hàm số có cực đại và cực tiểu thì m≠ 0.
+ Giả sử hàm số có hai điểm cực trị là: A( 0; 4m3) ; B( 2m; 0) ; A B → = ( 2 m ; - 4 m 3 )
Trung điểm của đoạn AB là I (m; 2m3).
+ Điều kiện để đối xứng nhau qua đường thẳng x- y= 0 hay y= x là AB vuông góc với đường thẳng y= x và I ∈ ( d ) ⇔ 2 m - 4 m 3 = 0 2 m 3 = m
⇔ m = 0 h o ặ c m = ± 2 2
Kết hợp với điều kiện ta có: m = ± 2 2 .
Chọn D.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
m
x
2
+
4
m
3
có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng
(...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 m x 2 + 4 m 3 có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng ( d ) : y = x .
A. m = 2 2
B. m = - 2 2
C. m = 0 h o ặ c m = 2 2 .
D. m = ± 2 2
Chọn D
y ' = 3 x 2 - 6 m x
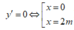
Để hàm số có cực đại và cực tiểu thì m ≠ 0
Giả sử hàm số có hai điểm cực trị là
![]()
Trung điểm của đoạn AB là I ( m ; 2 m 3 )
Điều kiện để AB đối xứng nhau qua đường thẳng y = x là AB vuông góc với đường thẳng
( d ) : y = x v à I ∈ ( d )
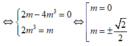
Kết hợp với điều kiện ta có m = ± 2 2
Đúng 0
Bình luận (0)



