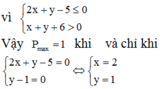tìm các giá trị nguyên của x,y thỏa mãn : x^3 + x^2 + 3x + 3 = y^3
VQ
Những câu hỏi liên quan
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
Đúng 0
Bình luận (0)
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Hai chữ số tận cùng của 51^51 2. Trung bình cộng của các giá trị của x thỏa mãn: (x - 2)^8 (x - 2)^6 3. Số x âm thỏa mãn: 5^(x - 2).(x + 3) 1 4. Số nguyên tố x thỏa mãn: (x - 7)^x+1 - (x - 7)^x+11 0 5. Tổng 3 số x,y,y biết: 2x y; 3y 2z và 4x - 3y + 2z 36 6. Tập hợp các số hữu tỉ x thỏa mãn đẳng thức: x^2 - 25.x^4 0 7. Giá trị của x trong tỉ lệ thức: 3x+2/5x+7 3x-1/5x+1 8. Giá trị của x thỏa mãn: (3x - 2)^5 -243 9. Tổng của 2 số x,y thỏa mãn: !x-2007! !y-2008! hoặc 0 10. số hữu tỉ dư...
Đọc tiếp
Hai chữ số tận cùng của 51^51
2. Trung bình cộng của các giá trị của x thỏa mãn: (x - 2)^8 = (x - 2)^6
3. Số x âm thỏa mãn: 5^(x - 2).(x + 3) = 1
4. Số nguyên tố x thỏa mãn: (x - 7)^x+1 - (x - 7)^x+11 = 0
5. Tổng 3 số x,y,y biết: 2x = y; 3y = 2z và 4x - 3y + 2z = 36
6. Tập hợp các số hữu tỉ x thỏa mãn đẳng thức: x^2 - 25.x^4 = 0
7. Giá trị của x trong tỉ lệ thức: 3x+2/5x+7 = 3x-1/5x+1
8. Giá trị của x thỏa mãn: (3x - 2)^5 = -243
9. Tổng của 2 số x,y thỏa mãn: !x-2007! = !y-2008! < hoặc = 0
10. số hữu tỉ dương và âm x thỏa mãn: (2x - 3)^2 = 16
11. Tập hợp các giá trị của x thỏa mãn đẳng thức: x^6 = 9.x^4
12. Số hữu tỉ x thỏa mãn: |x|. |x^2+3/4| = X
có khùng hk vậy hùng tự đăng tự giải ls
Đúng 0
Bình luận (0)
1) Quy luật cứ mũ chẵn 2 số tận cùng là 01 còn mũ lẻ thì 2 số tận cùng là 51
Vậy 2 số tận cùng của 51^51 là 51
2)pt<=> x-2=0 hoặc (x-2)^2=1 <=> x=2 hoặc x=1 hoặc x=3
Vậy trung bìng cộng là 2
4)Pt<=> (x-7)^(x+1)=0 hoặc 1-(x-7)^10=0=> x=7 hoặc x=8 hoặc x=6
Do x là số nguyên tố => x=7 TM
5)3y=2z=> 2z-3y=0
4x-3y+2z=36=> 4x=36=> x=9
=> y=2.9=18=> z=3.18/2=27
=> x+y+z=9+18+27=54
6)pt<=> x^2=0 hoặc x^2=25 <=> x=0 hoặc x=-5 hoặc x=5
7)pt<=> (3x+2)(5x+1)=(3x-1)(5x+7)
Nhân ra kết quả cuối cùng là x=3
8)ta có (3x-2)^5=-243=-3^5
=> 3x-2=-3 => x=-1/3
9)Câu này chưa rõ ý bạn muốn hỏi!
10)2x-3=4 hoặc 2x-3=-4
<=> x=7/2 hoặc x=-1/2
11)x^4=0 hoặc x^2=9
=> x=0 hoặc x=-3 hoặc x=3
Đúng 0
Bình luận (0)
anh đang chia sẻ kiến thức đóa à
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. cho x,y là các số dương thỏa mãn x + y < (h) = 1 .Tìm giá trị nhỏ nhất của biểu thức : A= \(\frac{1}{x^3+3xy^2}\)+\(\frac{1}{y^3+3x^2y}\)
2. a phân tích thành nhân tử (x+y)^2-(x+y)-6
b tìm các cặp giá trị (x;y) nguyên thỏa mãn phương trình sau:
2x^2 -x(2y-1)=y+12
1. Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\) với \(a=x^3+3xy^2,b=y^3+3x^2y\) (a;b > 0)
(Bất đẳng thức này a;b > 0 mới dùng được)
\(A\ge\frac{4}{x^3+3xy^2+y^3+3x^2y}=\frac{4}{\left(x+y\right)^3}\ge\frac{4}{1^3}=4\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x^3+3xy^2=y^3+3x^2y\\x+y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x^3-3x^2y+3xy^2-y^3=0\\x+y=1\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x-y\right)^3=0\\x+y=1\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
1)CÁC GIÁ TRỊ CỦA X;Y THUỘC Q THỎA MÃN |X-7/5|+|2,4-Y| LỚN HƠN HOẶC BẰNG 0. TÌM X;Y
2)GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC B=|4X-3|+|5Y+7,5|+17,5
3) GIÁ TRỊ CỦA BIỂU THỨC B=(1000-1^3).(1000-2^3).(1000-3^3).........(1000-50^3)
4)CÁC SỐ X,Y,Z THỎA MÃN (3X-5)^2006+(Y^2-1)^2008+(X-Z)^2100=0 LÀ ?
1 : Số các số nguyên ( x ; y ) thỏa mãn ( x - 1 )^2 3 là : .....2 : Số các số nguyên dương x thỏa mãn x/4 197/x + 2 là : ....3 : Giá trị nhỏ nhất của A giá trị tuỵt đối của x + 3 + giá trị tuyệt đối của x - 7 là : ....4 : Số các số nguyên của x để P giá trị tuyệt đối của 3x - 18 - giải trị tuyệt đối của 3x + 7 là : .....5 : Số bộ ba số nguyên tố ( a ; b ; c ) khcs nhau mà a.b.c a.b +b.c +a.c là ?
Đọc tiếp
1 : Số các số nguyên ( x ; y ) thỏa mãn ( x - 1 )^2 = 3 là : .....
2 : Số các số nguyên dương x thỏa mãn x/4 = 197/x + 2 là : ....
3 : Giá trị nhỏ nhất của A = giá trị tuỵt đối của x + 3 + giá trị tuyệt đối của x - 7 là : ....
4 : Số các số nguyên của x để P = giá trị tuyệt đối của 3x - 18 - giải trị tuyệt đối của 3x + 7 là : .....
5 : Số bộ ba số nguyên tố ( a ; b ; c ) khcs nhau mà a.b.c < a.b +b.c +a.c là ?
1, Tìm các số nguyên x,y thỏa mãn: x2 + 2xy + 7(x+y) +2y2 +10 = 0
2, Cho đa thức f(x) = x3-3x2+3x-4. Với giá trị nguyên nào của x thì giá trị của đa thức f(x) chia hết cho giá trị của đa thức x2 + 2.
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x(x - 3) + y(y - 3) + xy. Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6
A. Pmax = 0
B. Pmax = 2
C. Pmax = 1
D. Pmax = 3
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
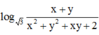
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
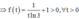
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 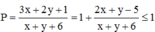
vì 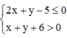
Vậy Pmax = 1 khi và chỉ khi 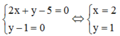
Đúng 0
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
(
x
-
3
)
+...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y
Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
![]()
![]()
![]()
![]()
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y . Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6
A. Pmax = 0
B. Pmax = 2
C. Pmax = 1
D. Pmax = 3
Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
![]()
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
![]()
![]()
![]()
Khi đó, 
vì 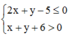
Vậy Pmax = 1 khi và chỉ khi 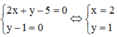
Đúng 0
Bình luận (0)