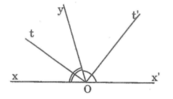
CMR: tia phân giác của 2 góc kề bù thì tạo thành 1 góc vuông
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TN
Những câu hỏi liên quan
CMR:2 tia phân giác của 2 góc kề bù tạo thành 1 góc vuông
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy vẽ hai góc xOy và yOx’ kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là mº.
Chứng minh rằng: Hai tia phân giác của 2 góc kề bù tạo thành 1 góc vuông
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
hình tự vẽ nha
Đúng 0
Bình luận (0)
Giải thích tại sao hai tia phân giác của hai góc kề bù thì tạo thành một góc vuông.
Theo mình thì góc kề bù là góc vừa kề vừa bù thì = 180o và chung một cạnh mà hai tia phân giác của hai góc kề bù sẽ tạo thành một góc vuông.
Mình hiểu nhưng khó nói lắm.
Đúng 0
Bình luận (0)
gọi số đo 2 góc kề bù là a và b=>a+b=180 độ
=>2 tia p/g của góc đó tạo thành một góc có số đo là:1/2.a+1/2.b=1/2(a+b)=1/2.180độ=90độ
Để gải chi tiết bài này phải vẽ hình
Bài làm chỉ mang T/C gt
Đúng 0
Bình luận (0)
CMR:
1. Tia phân giác của 2 góc kề bù thì vuông góc với nhau.
2. Tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau
Chứng minh định lí:
Hai tia phân giác của hai góc kề bù thì tạo thành góc vuông
Ta có \(A_1=A_2;A_3=A_4\)
Có \(A_1+A_2+A_3+A_4=180\)
\(\Rightarrow2\left(A_2+A_3\right)=180\)
\(\Rightarrow A_2+A_3=90\)
Đúng 1
Bình luận (0)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 1
Bình luận (0)
Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Fan TFboys phải không?...mình cũng vậy
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho gốc xOz .GoijOy lầ tia phân giác góc xOz.Gọi Ot là tia phân giác của góc xOy .Tìm giá trị lớn nhất của góc xOt .Chứng ttor rằng 2 tia phân giác của 2 góc kề bù tạo thành 1 góc vuông
CMR : 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
cho: xOy và yOz là 2 góc kề bù, om là p/giác xOy, on là p/giác yOz. ta có:
xOy+yOz=1800
=> 1/2(xOy+yOz)=900
=> 1/2xOy+1/2yOz=900
=> mOy+yOn=900
=> 2 tia p/giác của 2 góc kề bù thì vuông góc với nhau
Đúng 0
Bình luận (0)
Bài 4: CMR 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 0
Bình luận (0)
Ta gọi góc xOy và yOz là hai góc kề bù. Ot là tia phân giác của góc xOy, Ot' là tia phân giác của góc yOx
Hình bn tự vẽ nhé ( Số liệu tùy ý )
Ta có : \(\widehat{xOy}+\widehat{yoz}=180^0\)
Vì Ot là tia phân giác của góc xOy => \(\widehat{yOt}=\frac{\widehat{xOy}}{2}\)
Vì Oy' là tia phân giác của góc yOz => \(\widehat{yOt'}=\frac{\widehat{yOz}}{2}\)
=> \(\widehat{yOt}+\widehat{yOt'}=\frac{\widehat{xOy}+\widehat{yOz}}{2}=\frac{180^0}{2}=90^0\)
=> Góc tOt' = 900 => Góc tOt' là góc vuông.
Vậy : Góc tạo thành bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời