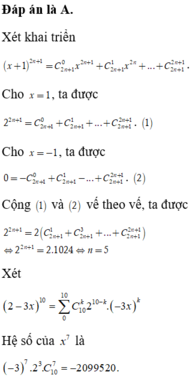tìm số nguyên dương n thỏa mãn Cn+12n+1 + C2n+1n+2 +....+C2n +12n + C2n+12n +1 =236
HT
Những câu hỏi liên quan
Tìm số nguyên dương n thỏa mãn
C
2
n
+
1
1
+
C
2
n
+
1
3
+
.
.
.
+
C
2
n
+
1
2
n...
Đọc tiếp
Tìm số nguyên dương n thỏa mãn C 2 n + 1 1 + C 2 n + 1 3 + . . . + C 2 n + 1 2 n + 1 = 1024
A. n = 10
B. n = 5
C. n = 9
D. n = 11
Tìm số nguyên dương n thỏa mãn
C
2
n
+
1
1
+
C
2
n
+
1
3
+
...
+
C
2
n
+
1
2
n...
Đọc tiếp
Tìm số nguyên dương n thỏa mãn C 2 n + 1 1 + C 2 n + 1 3 + ... + C 2 n + 1 2 n + 1 = 1024
A.n =5
B.n =9
C.n =10
D.n= 4
Xét khai triển x + 1 2 n + 1 = C 2 n + 1 0 x 2 n + 1 + C 2 n + 1 1 x 2 n + ... + C 2 n + 1 2 n + 1 .
Cho x =1 , ta được 2 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 .(1)
Cho x= -1, ta được 0 = − C 2 n + 1 0 + C 2 n + 1 1 − ... + C 2 n + 1 2 n + 1 . (2)
Cộng (1) và (2) vế theo vế, ta được :
2 2 n + 1 = 2 C 2 n + 1 1 + C 2 n + 1 3 + ... + C 2 n + 1 2 n + 1 ⇔ 2 2 n + 1 = 2.1024 = 2 11 ⇔ 2 n + 1 = 11 ⇔ n = 5 .
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho khai triển nhị thức Newton của
2
−
3
x
2
n
, biết rằng n là số nguyên dương thỏa mãn
C
2
n
+
1
1
+
C
2
n
+
1...
Đọc tiếp
Cho khai triển nhị thức Newton của 2 − 3 x 2 n , biết rằng n là số nguyên dương thỏa mãn C 2 n + 1 1 + C 2 n + 1 3 + C 2 n + 1 5 + ... + C 2 n + 1 2 n + 1 = 1024. .
Hệ số của x 7 bằng
A. -2099520
B. -414720
C. 2099520
D. 414720
Đáp án là A
• Xét khai triển:
x + 1 2 n + 1 = C 2 n + 1 0 x 2 n + 1 + C 2 n + 1 1 x 2 n + ... + C 2 n + 1 2 n + 1 .
Cho x = 1 , ta được: 2 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 . (1)
Cho x = − 1 , ta được: 0 = − C 2 n + 1 0 + C 2 n + 1 1 − ... + C 2 n + 1 2 n + 1 . (2)
Cộng (1) và (2) vế theo vế, ta được:
2 2 n + 1 = 2 C 2 n + 1 1 + C 2 n + 1 3 + ... + C 2 n + 1 2 n + 1 ⇔ 2 2 n + 1 = 2.1024 ⇔ n = 5
• Xét: 2 − 3 x 10 = ∑ 0 10 C 10 k 2 10 − k . − 3 x k = ∑ 0 10 − 3 k .2 10 − k . C 10 k . x k
Hệ số của x 7 là: − 3 7 .2 3 . C 10 7 = − 2099520.
Đúng 0
Bình luận (0)
Cho khai triển nhị thức Newton của
2
-
3
x
2
n
, biết rằng n là số nguyên dương thỏa mãn
C
2
n
+
1
1
+
C
2...
Đọc tiếp
Cho khai triển nhị thức Newton của 2 - 3 x 2 n , biết rằng n là số nguyên dương thỏa mãn C 2 n + 1 1 + C 2 n + 1 3 + C 2 n + 1 5 + . . . + C 2 n + 1 2 n + 1 = 1024 .
Hệ số của x 7 bằng
A. -2099520
B. -414720
C. 2099520
D. 414720
Tìm số nguyên dương n sao cho
C
2
n
+
1
1
-
2
.
2
.
C
2
n
+
1
2
+
3
.
2
2
.
C
2
n
+...
Đọc tiếp
Tìm số nguyên dương n sao cho C 2 n + 1 1 - 2 . 2 . C 2 n + 1 2 + 3 . 2 2 . C 2 n + 1 3 - 4 . 2 3 . C 2 n + 1 4 + . . . + ( 2 n + 1 ) 2 2 n . C 2 n + 1 2 n + 1 = 2019
A. 1009
B. 1010
C. 1011
D. 1012
Tìm số nguyên dương n sao cho:
C
2
n
+
1
1
-
2
.
2
.
C
2
n
+
1
2
+
3
.
2
2
.
C
2
n
+...
Đọc tiếp
Tìm số nguyên dương n sao cho:
C 2 n + 1 1 - 2 . 2 . C 2 n + 1 2 + 3 . 2 2 . C 2 n + 1 3 - 4 . 2 3 . C 2 n + 1 4 + . . . + ( 2 n + 1 ) . 2 2 n . C 2 n + 1 2 n + 1 = 2017
A. n = 1005.
B. n = 1006.
C. n = 1007.
D. n = 1008.
Chọn D.
Với ∀x ∈ R ta có: ![]()
![]()
Lấy đạo hàm hai vế theo x ta được:
![]()
![]()
Thay x = -2 vào (1) ta được:
![]()
Từ yêu cầu bài toán ta có: 2n + 1 2017 ⇔ n = 2018.
Đúng 0
Bình luận (0)
Tìm số nguyên dương n sao cho
C
2
n
+
1
1
-
2
.
2
.
C
2
n
+
1
2
+
3
.
2
.
C
2
n
+
1...
Đọc tiếp
Tìm số nguyên dương n sao cho
C 2 n + 1 1 - 2 . 2 . C 2 n + 1 2 + 3 . 2 . C 2 n + 1 3 - 4 . 2 3 . C 2 n + 1 4 + . . + 2 n + 1 2 2 n C 2 n + 1 2 n + 1 = 2019
A. 1009
B. 1010
C. 1011
D. 1012
Xét khai triển
1 + x 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 x + C 2 n + 1 2 x 2 + C 2 n + 1 3 x 3 + C 2 n + 1 4 x 4 + . . . + C 2 n + 1 2 n + 1 x 2 n + 1
Lấy đạo hàm cả hai vế ta được
2 n + 1 x 2 n = C 2 n + 1 1 - 2 x C 2 n + 1 2 + 3 x 2 C 2 n + 1 3 - 4 x 3 . C 2 n + 1 4 + . . + 2 n + 1 x 2 n C 2 n + 1 2 n + 1
Thay x = -2 vào ta được
2 n + 1 x 2 n = C 2 n + 1 1 + 2 x . 2 . C 2 n + 1 2 + 3 x 2 C 2 n + 1 3 - 4 x 3 C 2 n + 1 4 + . . + 2 n + 1 x 2 n C 2 n + 1 2 n + 1
Kết hợp với giả thiết bài toán ta được: 2 n + 1 = 2019 ⇔ n = 2019
Vậy n = 1009 là giá trị cần tìm
Đáp án A
Đúng 0
Bình luận (0)
Tìm số nguyên dương n sao cho
C
2
n
+
1
1
-
2
.
2
C
2
n
+
1
2
+
3
.
2
2
.
C...
Đọc tiếp
Tìm số nguyên dương n sao cho C 2 n + 1 1 - 2 . 2 C 2 n + 1 2 + 3 . 2 2 . C 2 n + 1 3 - . . . + 2 n + 1 . 2 n . C 2 n + 1 2 n + 1 = 2005
![]()
![]()
![]()
![]()
Tìm số nguyên dương n sao cho
C
2
n
+
1
1
−
2.2
C
2
n
+
1
2
+
3.2
2
.
C
2
n
+
1
2...
Đọc tiếp
Tìm số nguyên dương n sao cho C 2 n + 1 1 − 2.2 C 2 n + 1 2 + 3.2 2 . C 2 n + 1 2 − ... + 2 n + 1 2 n C 2 n + 1 2 n + 1 = 2005.
A. n = 1002
B. n = 1114
C. n = 102
D. n = 1001
Chọn A.
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton:
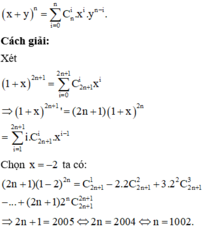
Đúng 0
Bình luận (0)
Tìm số nguyên dương n thỏa mãn
C
2
n
+
1
1
+
C
2
n
+
1
2
+
...
+
C
2
n
+
1
n
2...
Đọc tiếp
Tìm số nguyên dương n thỏa mãn C 2 n + 1 1 + C 2 n + 1 2 + ... + C 2 n + 1 n = 2 20 − 1
A.n= 8
B.n = 9
C.n =10
D. n =11
Ta có 2 2 n + 1 = 1 + 1 2 n + 1 = C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 2 n + 1 . (1)
Lại có C 2 n + 1 0 = C 2 n + 1 2 n + 1 ; C 2 n + 1 1 = C 2 n + 1 2 n ; C 2 n + 1 2 = C 2 n + 1 2 n − 1 ; . . . ; C 2 n + 1 n = C 2 n + 1 n + 1 . (2)
Từ (1) và (2), suy ra C 2 n + 1 0 + C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n + 1 2
⇔ C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n + 1 2 − C 2 n + 1 0
⇔ C 2 n + 1 1 + ... + C 2 n + 1 n = 2 2 n − 1 ⇔ 2 20 − 1 = 2 2 n − 1 ⇔ n = 10 .
Vậy n =10 thỏa mãn yêu cầu bài toán.
Chọn đáp án C.
Đúng 0
Bình luận (0)