Chứng minh tổng 4 góc trong 1 tứ giác bằng 360 độ ( không dùng cách kẻ đường chéo nhé )
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NG
Những câu hỏi liên quan
Chứng minh định lí tổng 4 góc của 1 tứ giác bằng 360 ( không dùng cách kẻ đường chéo)
chứng minh tổng 4 góc của tứ giác= 360do k dùng cách cm bằng đg chéo của tứ giác ?
theo như mình biết thì, tứ giác vẽ môt đường chéo sẽ ra hai hình tam giác cộng lại bằng 360 độ. Vậy nếu kẻ hai đường chéo thì sao nó vận bằng 360 độ vì bây giờ đã là 4 hình tam giác rồi?
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A70 độ , góc D80 độ và góc ngoài ở đỉnh C60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D 90 độ. Chứng minh rằng AC2+ BD2 AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cả...
Đọc tiếp
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A=70 độ , góc D=80 độ và góc ngoài ở đỉnh C=60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D= 90 độ. Chứng minh rằng AC2+ BD2= AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cảm ơn các bạn
Bài 1: 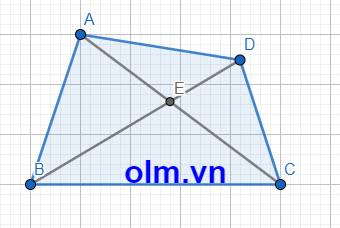
Gọi E là giao điểm của hai đường chéo AC và BD
Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC
(AE + CE) + (BE + DE) > AB + DC
AC + BD > AB + DC
Tương tự ta có AC + BD > AD + BC
Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.
Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)
Theo chứng minh trên ta có:
\(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)
Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:
AB + AD > BD
AB + BC > AC
BC + CD > BD
CD + AD > AC
Cộng vế với vế ta có:
(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2
⇒AB + BC + CD + DA > BD + AC (2)
Kết hợp (1) và (2) ta có:
Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác
Đúng 0
Bình luận (0)
Bài : 2 Góc C = 1800 - 600 = 1200
Tổng bốn góc của tứ giác là 3600
Ta có: Góc B của tứ giác ABCD là:
3600 - (700 + 800 + 1200) = 900
Câu b chứng minh như bài 1
Đúng 0
Bình luận (0)
Bài 1:
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.
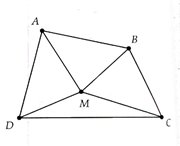
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD
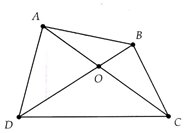
Bài 3:
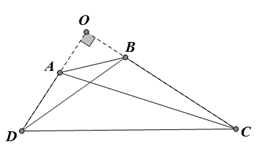
Gọi O là giao điểm AD và BC.
Ta có nên
Áp dụng định lí Py – ta – go,
Ta có
Nên
Đúng 0
Bình luận (0)
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A70 độ , góc D80 độ và góc ngoài ở đỉnh C60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D 90 độ. Chứng minh rằng AC2+ BD2 AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cả...
Đọc tiếp
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A=70 độ , góc D=80 độ và góc ngoài ở đỉnh C=60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D= 90 độ. Chứng minh rằng AC2+ BD2= AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cảm ơn các bạn
Cho tứ giác ABCD có góc A 70 độ, góc D 80 độ và góc ngoài ở đỉnh C 60 độ.
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng 2 đường chéo luôn lớn hơn tổng 2 cạnh đối của tứ giác đó.
Mọi người giúp mình nhé!
Chứng minh rằng trong tứ giác tổng 2 đường chéo lớn hơn tổng hai cạnh đối
Cho tứ giác có AB =BC , góc A + góc C = 180 độ . Chứng minh rằng BD là tia phân giác của Tam giác ADC
a, Gọi AC giao BD tai O
TAm giác OAB có
OA + OB > AB (1)
Tam giác OCD có
OC + OD > CD (2)
cộng vế với vế của (1) và (2) -=> AC + BD > AB + CD
Đúng 0
Bình luận (0)
Mình cũng đồng ý với ý kiến của bạn
Đúng 0
Bình luận (0)
đúng nhưng bạn thiếu rồi
còn AC+BD>AD+BC nữa
Đúng 0
Bình luận (0)
tính các góc của tứ giác ABCD biết ^A:^B:^C:^D=1:2:3:4. Từ đó chứng minh tổng các góc ngoài của tứ giác =360 độ
Chứng minh rằng trong tứ giác tổng 2 đường chéo lớn hơn tổng hai cạnh đối
Cho tứ giác có AB =BC , góc A + góc C = 180 độ . Chứng minh rằng BD là tia phân giác của Tam giác ADC
P/s : ko can ve hinh dau

