CMR 2110-1 chia hết cho 200
Chứng tỏ rằng 21 10 – 1 chia hết cho 200
* Áp dụng hằng đẳng thức:
![]()
Ta có:
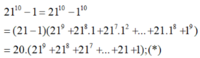
Ta có:
![]()
![]()
gồm có 10 số hạng
![]()
có chữ số tận cùng bằng 0. Do đó, ta có thể viết:
![]()
Thay vào (*) ta được:
2110 - 1 = 20.10.A = 200A
Suy ra: 2110 - 1 chia hết cho 200.
Chứng minh rằng
a) 2110−1chia hết cho 200
b) 3930+3913chia hết cho 40
c) 260+530chia hết cho 41
link tham khảo
ccaau hỏi của ng duy mạnh
link : https://olm.vn/hoi-dap/detail/60197622644.html
hok tót
chứng minh \(2^{2^{2n+1}}\)+2110 chia hết cho 7
cmr:2110-1 chia hết cho 200
cho x thuộc Z. CMR: x^200+x+100+1 chia hết x^4+x^2+1
https://vn.answers.yahoo.com/question/index?qid=20111212062832AACt3bZ
bài 1: Cmr
a,2110-1 chia hết cho 200
Ta có: 212=441 đồng dư với 1(mod 200)
=>212 đồng dư với 1(mod 200)
=>(212)5 đồng dư với 15(mod 200)
=>2110 đồng dư với 1(mod 200)
=>2110-1 đồng dư với 1-1=0(mod 200)
=>2110-1 đồng dư với 0(mod 200)
=>2110-1 chia hết cho 200
cho x thuộc Z. CMR: x^200+x+100+1 chia hết x^4+x^2+1
Ta có : x6n-1=(x6-1).A=(x2-1)(x4+x2+1)A chia hết cho x4 + x2 +1
Khi đó : M=x200+x100+1=x200-x2+x100-x4+(x4+x2+1)= x2[(x6)33-1]-x4 [(x6)16-1]+(x4 + x2 +1)
Vì x2[(x6)33-1]chia hết cho x4 + x2 +1
x4 [(x6)16-1]chia hết cho x4 + x2 +1
Nên .....
cho x thuộc Z. CMR: x^200+x+100+1 chia hết x^4+x^2+1
CMR:
a, 101 x 102 x 103 x..x 200 chia hết cho 1 x 3 x 5 x...x 199.
b, 201 x 202 x 203 x...x 600 chia hết cho 3200