Hãy biểu diễn dao động điều hòa X = 3 cos (5t +\(\frac{\pi}{3}\)(cm) bằng 1 vecto quay.
KM
Những câu hỏi liên quan
Vecto quay biểu diễn dao động điều hòa
x
4
,
5
cos
4
π
t
+
π
8
(trong đó x tính bằng cm, t tính bằng giây) có: A. tốc độ góc 4 rad/s. B. chiều dài 4,5 cm. C. chiều dài 9 cm. D. tần số
4
π
Hz.
Đọc tiếp
Vecto quay biểu diễn dao động điều hòa x = 4 , 5 cos 4 π t + π 8 (trong đó x tính bằng cm, t tính bằng giây) có:
A. tốc độ góc 4 rad/s.
B. chiều dài 4,5 cm.
C. chiều dài 9 cm.
D. tần số 4 π Hz.
Đáp án B
Vecto quay biễu diễn dao động điều hòa có chiều dài 4,5 cm
Đúng 0
Bình luận (0)
Vecto quay biểu diễn dao động điều hòa
x
4
,
5
cos
(
4
πt
+
π
8
)
(trong đó x tính bằng cm, t tính bằng giây) có: A. tốc độ góc 4 rad/s. B. chiều dài 4,5 cm. C. chiều dài 9 cm. D. tần số
4
π
Hz.
Đọc tiếp
Vecto quay biểu diễn dao động điều hòa x = 4 , 5 cos ( 4 πt + π 8 ) (trong đó x tính bằng cm, t tính bằng giây) có:
A. tốc độ góc 4 rad/s.
B. chiều dài 4,5 cm.
C. chiều dài 9 cm.
D. tần số 4 π Hz.
+ Vecto quay biễu diễn dao động điều hòa có chiều dài 4,5 cm.
Đáp án B
Đúng 0
Bình luận (0)
Nêu cách biểu diễn một dao động điều hòa bằng một vecto quay.
Mỗi dao động điều hòa x = Acos(ωt + φ) được biểu diễn bằng một vecto quay. Vecto quay có đặc điểm:
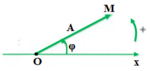
Có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu φ (chọn chiều dương là chiều của đường tròn lượng giác)
Đúng 0
Bình luận (0)
Nêu cách biểu diễn một dao động điều hòa bằng một vecto quay.
Biểu diễn dao động điều hòa có phương trình: x = Acos(ωt + Ø) (*)
Các bước:
+ Vẽ trục tọa độ Ox nằm ngang
+ Vẽ vecto OM 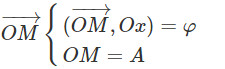
+ Khi t = 0 ,cho vecto OM quay đều quanh O với tốc độ góc ω.
Khi đó, vecto quay OM biểu diễn dao động điều hòa có phương trình (*)
Đúng 0
Bình luận (0)
Hai dao động điều hòa có phương trình
x
1
A
1
cos
ω
1
t và
x
2
A
2
cosω
2
t
được biểu diễn trong một hệ tọa độ vuông góc xOy tương ứng bằng hai vecto quay
A
→
1...
Đọc tiếp
Hai dao động điều hòa có phương trình x 1 = A 1 cos ω 1 t và x 2 = A 2 cosω 2 t được biểu diễn trong một hệ tọa độ vuông góc xOy tương ứng bằng hai vecto quay A → 1 và A → 2 . Trong cùng một khoảng thời gian, góc mà hai vecto A → 1 và A → 2 quay quanh O lần lượt là a và b = 6,1a. Tỉ số ω 1 ω 2 bằng
A. 0,9.
B. 6,1.
C. 5,1
D. 0,16
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình
\(x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\)
Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimet. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Vật đi qua vị trí cân bằng thì x = 0
Khi đó
\(\begin{array}{l}2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \\\Leftrightarrow t = \frac{2\pi }{15} + \frac{{k\pi }}{5} ;k \in Z\end{array}\)
Do khoảng thời gian từ 0 đến 6 giây nên \(t \in \left[ {0;6} \right]\)
\(\begin{array}{l}0 \le \ \frac{{2\pi }}{{15}} + \frac{{k\pi }}{5} \le \ 6;k \in Z\\ \Rightarrow \frac{-2 }{3}\le \ k \le \ \frac{90 - 2\pi}{3\pi};k \in Z\end{array}\)
Do \(k \in Z\) nên \(k \in \left\{ {0;1;2;3;4;5;6;7;8} \right\}\)
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.
Đúng 0
Bình luận (0)
1. Một chất điểm dao động điều hòa có phương trình li độ theo thời gian là x 5sqrt{3} cos(10pit + dfrac{pi}{3} )(cm) . Tần số của dao động bằng:
A. 10Hz B. 20Hz C. 10piHz D. 5Hz
2. Một chất điểm dao động điều hòa có phương trình li độ theo thời gian là x 6cos(4pit + dfrac{pi}{3} ) (cm) . chu kì của dao động bằng:
A. 4s B. 2s C. 0,25s D. 0,5s
Đọc tiếp
1. Một chất điểm dao động điều hòa có phương trình li độ theo thời gian là x= 5\(\sqrt{3}\) cos(10\(\pi\)t + \(\dfrac{\pi}{3}\) )(cm) . Tần số của dao động bằng:
A. 10Hz B. 20Hz C. 10\(\pi\)Hz D. 5Hz
2. Một chất điểm dao động điều hòa có phương trình li độ theo thời gian là x= 6cos(4\(\pi\)t + \(\dfrac{\pi}{3}\) ) (cm) . chu kì của dao động bằng:
A. 4s B. 2s C. 0,25s D. 0,5s
Xét một vecto quay OM→ có những đặc điểm sau: - Có độ lớn bằng hai đơn vị chiều dài. - Quay quanh O với tốc độ góc 1 rad/s - Tại thời điểm t 0, vecto OM→ hợp với trục Ox một góc 30o Hỏi vecto quay OM→ biểu diễn phương trình của dao động điều hòa nào? A. x 2cos(t – π/3) B. x 2cos(t + π/6) C. x 2cos(t - 30o) D. x 2cos(t + π/3)
Đọc tiếp
Xét một vecto quay OM→ có những đặc điểm sau:
- Có độ lớn bằng hai đơn vị chiều dài.
- Quay quanh O với tốc độ góc 1 rad/s
- Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o
Hỏi vecto quay OM→ biểu diễn phương trình của dao động điều hòa nào?
A. x = 2cos(t – π/3) B. x = 2cos(t + π/6)
C. x = 2cos(t - 30o) D. x = 2cos(t + π/3)
Chọn đáp án B.
Vecto quay OM→ có:
+ Có độ lớn bằng hai đơn vị chiều dài nên biên độ dao động A = 2.
+ Quay quanh O với tốc độ góc 1 rad/s nên tần số ω = 1rad/s.
+ Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o nên pha ban đầu là φ = π/6 rad.
Phương trình dao động: x = 2.cos(t + π/6).
Đúng 0
Bình luận (0)
Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ 5 cm, chu kì 2 s. Tại thời điểm t 0, vật đi qua cân bằng O theo chiều dương. Phương trình dao động của vật làA.x 5cos(pi t - frac{pi}{2})(cm)B.x 5cos(2pi t - frac{pi}{2})(cm)C.x 5cos(2pi t + frac{pi}{2})(cm)D.x 5cos(pi t + frac{pi}{2})(cm)
Đọc tiếp
Một vật nhỏ dao động điều hòa dọc theo trục Ox với biên độ 5 cm, chu kì 2 s. Tại thời điểm t = 0, vật đi qua cân bằng O theo chiều dương. Phương trình dao động của vật là
A.\(x = 5\cos(\pi t - \frac{\pi}{2})\)(cm)
B.\(x = 5\cos(2\pi t - \frac{\pi}{2})\)(cm)
C.\(x = 5\cos(2\pi t + \frac{\pi}{2})\)(cm)
D.\(x = 5\cos(\pi t + \frac{\pi}{2})\)(cm)
Phương trình tổng quát: \(x= A cos(\omega t+\varphi)\)
+ Tần số góc: \(\omega = 2\pi/2 = \pi \ (rad/s)\)
+ t=0, vật qua VTCB theo chiều đương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ cm\\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình dao động: \(x = 5\cos(\pi t - \frac{\pi}{2})\) (cm)
Đúng 0
Bình luận (1)


