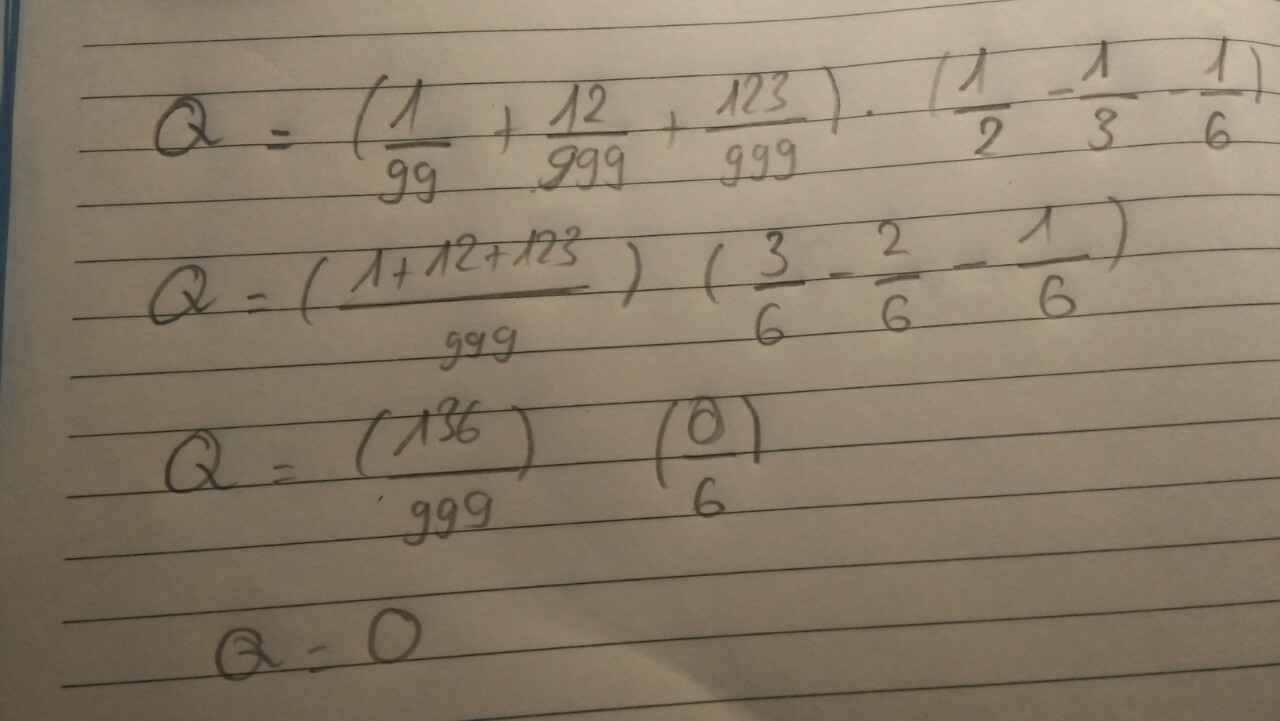tính giá trị biểu thức : Q=(1/99+12/999+123/999)(1/2-1/3-1/6)
H24
Những câu hỏi liên quan
tính giá trị của biểu thức: Q = (1/99+12/999+123/999). (1/2-1/3-1/6)
Tính giá trị của biểu thức: Q =\((\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{999})\cdot(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6})\)
Tính giá trijcuar biểu thức
Q= (1/99 + 12/999 + 123/ 999 ). ( 1/2 -1/3- 1/6)
Có: \(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right).\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\)
\(=\left(\frac{1}{2}+\frac{12}{999}+\frac{123}{999}\right).\left(\frac{3}{6}-\frac{2}{6}-\frac{1}{6}\right)\)
\(=\left(\frac{1}{2}+\frac{12}{999}+\frac{123}{999}\right).0=0\)
Đúng 1
Bình luận (0)
Tính giá trị của biểu thức: \(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\cdot\dfrac{0}{6}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}+\dfrac{123}{9999}\right)\cdot0\)
\(Q=0\)
Đúng 1
Bình luận (0)
tính giá trị :\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right)\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\)
\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right)\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\text{ }\)
\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right)\left(\frac{3}{6}-\frac{2}{6}-\frac{1}{6}\right)\)
\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right).0\)
\(Q=0\)
Đúng 0
Bình luận (0)
Q=(1/99+12/999+123/999).(1/2-1/3-1/6) =(1/99+12/999+123/999).0 Q=0
Đúng 0
Bình luận (0)
\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right)\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\)
\(\Leftrightarrow Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right)\times0\)
\(\Leftrightarrow Q=0\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Rút gọn biểu thức:
A= 1+1/2+1/2^2+1/2^3+...+1/2^2012
B= ( 1/99+12/999+123/999)(1/2-1/3-1/6)
\(2A=2+1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2011}}\)
=> \(2A-A=\left(2+1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2011}}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2012}}\right)\)
=> \(A=2-\frac{1}{2^{2012}}=\frac{2^{2013}-1}{2^{2012}}\)
\(A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2012}}\)
\(2A=2\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2012}}\right)\)
\(2A=3+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2011}}\)
\(2A-A=A\)
\(=\left(3+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2011}}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2012}}\right)\)
\(=3+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{2011}}-1-\frac{1}{2}-\frac{1}{2^2}-\frac{1}{2^3}-...-\frac{1}{2^{2012}}\)
\(=2-\frac{1}{2012^2}\)
\(B=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{9999}\right)\cdot\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\)
\(B=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{9999}\right)\cdot\left(\frac{6}{12}-\frac{4}{12}-\frac{2}{12}\right)\)
\(B=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{9999}\right)\cdot0=0\)
q=(1/99+12/999+123/999)*(1/2-1/3-1/6)
q = (1/99+12/999+123/999)*(1/2-1/3-1/6)
= (1/99+12/999+123/999) * 0
= 0
Q= (1/99+12/999+123/999)(1/2-1/3-1/6)
\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right).\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\))
\(Q=\left(\frac{1}{99}+\frac{12}{999}+\frac{123}{999}\right).0=0\)
Đúng 1
Bình luận (0)
Q = (1/99 + 12/999 + 123/999) x (1/2 - 1/3 - 1/6)
Q=(1/99+12/999+123/999)x(1/6-1/6)
Q=(1/99+12/999+123/999)x0
Q=0
học tốt!
Đúng 1
Bình luận (0)