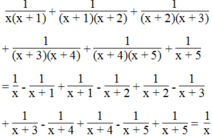a=1x!+2x!+3x!+4x!
ND
Những câu hỏi liên quan
Chứng minh:
1
x
x
+
1
+
1
x
+
1
x
+
2
+
1
x
+
2...
Đọc tiếp
Chứng minh:
1 x x + 1 + 1 x + 1 x + 2 + 1 x + 2 x + 3 + 1 x + 3 x + 4 + 1 x + 4 x + 5 + 1 x + 5
Giải các phương trình:
a)x−12+4x=25+2x−1x−12+4x=25+2x−1 b) x+2x+3x−19=3x+5;
a) x−12+4x=25+2x−1x−12+4x=25+2x−1
⇔5x – 12 = 2x + 24
⇔5x – 2x = 24 + 12
⇔3x = 36
⇔x = 12
Vậy phương trình có nghiệm x = 12.
b) x+2x+3x−19=3x+5x+2x+3x−19=3x+5
⇔6x – 19 = 5x +3x
⇔3x= 24
⇔x= 8
Vậy phương trình có nghiệm x = 8.
Đúng 0
Bình luận (0)
a) x−12+4x=25+2x−1x−12+4x=25+2x−1
⇔5x – 12 = 2x + 24
⇔5x – 2x = 24 + 12
⇔3x = 36
⇔x = 12
Vậy x=12 là nghiệm của phương trình
b) x+2x+3x−19=3x+5x+2x+3x−19=3x+5
⇔6x – 19 = 5x +3x
⇔3x= 24
⇔x= 8
Vậy x=8 là nghiệm của phương trình
Đúng 0
Bình luận (0)
Tìm số nguyên x, biết:a)
4
3
2
x
−
1
x
b)
2
x
−
1
3
3
x
+
1
4
c)
4
x...
Đọc tiếp
Tìm số nguyên x, biết:
a) 4 3 = 2 x − 1 x
b) 2 x − 1 3 = 3 x + 1 4
c) 4 x + 2 = 7 3 x + 1
d) − 3 x + 1 = 4 2 − 2 x
a) Không tồn tại x
b) x = -7
c) x = 2
d) x = 5
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a
)
5
x
-
3
2
4
x
-
7
2
*
b
)
96
x
2
-
16
+
6
2...
Đọc tiếp
Giải các phương trình sau:
a ) 5 x - 3 2 = 4 x - 7 2 * b ) 96 x 2 - 16 + 6 = 2 x - 1 x + 4 + 3 x - 1 x - 4 c ) 1 - x 2 x 2 - 4 x - 1 4 x - 4 = x - 1 2 x x - 2 - 1 2 x
a) (*) ⇔ (5x – 3)2 – (4x – 7)2 = 0
⇔ (5x – 3 + 4x – 7)(5x – 3 – 4x + 7) = 0
⇔ (9x – 10)(x + 4) = 0 ⇔ 9x – 10 = 0 hoặc x + 4 = 0
⇔ x = 10/9 hoặc x = -4
Tập nghiệm : S = { 10/9 ; -4}
b) ĐKXĐ: (x + 4)(x – 4) ≠ 0 ⇔ x + 4 ≠ 0 và x – 4 ≠ 0 ⇔ x ≠ ⇔ 4
Ta có: x2 – 16 = (x + 4)(x – 4) ≠ 0
Quy đồng và khử mẫu, ta được:
96 + 6(x2 – 16) = (2x – 1)(x – 4) + (3x – 1)(x + 4)
⇔ 96 + 6x2 – 96 = 2x2 – 8x – x + 4 + 3x2 + 12x – x – 4
⇔ x2 – 2x = 0 ⇔ x(x – 2) = 0
⇔ x = 0 hoặc x – 2 = 0
⇔ x = 0 hoặc x = 2 (thỏa mãn ĐKXĐ)
Tập nghiệm: S = {0;2}
c) ĐKXĐ: x ≠ 0; x – 1 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ 0; x ≠ 1 và x ≠ 2
MTC: 4x(x – 2)(x – 1)
Quy đồng và khử mẫu, ta được:
2(1 – x)(x – 1) – x(x – 2) = 2(x – 1)2 – 2(x – 1)(x – 2)
⇔ -2x2 + 4x – 2 – x2 + 2x = 2x2 – 4x + 2 – 2x2 + 6x – 4
⇔ 3x2 – 4x = 0 ⇔ x(3x – 4) = 0 ⇔ x = 0 hoặc x = 4/3
(x = 0 không thỏa mãn ĐKXĐ)
Tập nghiệm: S = {4/3}
Đúng 0
Bình luận (0)
Đố. Đố em tính nhanh được tổng sau:
1
x
x
+
1
+
1
x
+
1
x
+
2...
Đọc tiếp
Đố. Đố em tính nhanh được tổng sau:
1 x x + 1 + 1 x + 1 x + 2 + 1 x + 2 x + 3 + 1 x + 3 x + 4 + 1 x + 4 x + 5 + 1 x + 5 x + 6
Áp dụng kết quả Bài 31 a) (trang 50 SGK Toán 8 Tập 1) ta được:
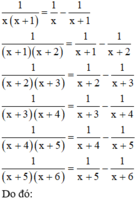
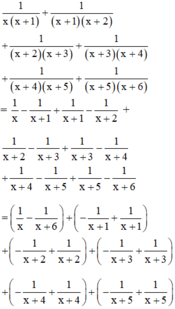
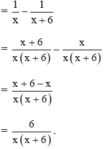
Đúng 0
Bình luận (0)
Giải các phương trình:
a) x−12+4x=25+2x−1x−12+4x=25+2x−1
b) x+2x+3x−19=3x+5;
a)x−12+4x=25+2x−1x−12+4x=25+2x−1
⇔5x – 12 = 2x + 24
⇔5x – 2x = 24 + 12
⇔3x = 36
⇔x = 12
Vậy phương trình có nghiệm x = 12.
b) x+2x+3x−19=3x+5x+2x+3x−19=3x+5
⇔6x – 19 = 5x +3x
⇔3x= 24
⇔x= 8
Vậy phương trình có nghiệm x = 8.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
3
x
-
1
x
-
1
-
2
x
+
5
x
+
3
1
-
4
x
-
1
x
+...
Đọc tiếp
Giải các phương trình sau: 3 x - 1 x - 1 - 2 x + 5 x + 3 = 1 - 4 x - 1 x + 3
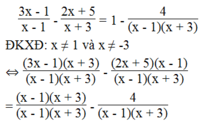
⇔ (3x – 1)(x + 3) – (2x + 5)(x – 1) = (x – 1)(x + 3) – 4
⇔ 3x2 + 9x – x – 3 – 2x2 + 2x – 5x + 5 = x2 + 3x – x – 3 – 4
⇔ 3x2 – 2x2 – x2 + 9x – x + 2x – 5x – 3x + x = -3 – 4 + 3 – 5
⇔ 3x = - 9 ⇔ x = - 3 (loại)
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
1X!+2x!+3x!+4x!
1x.2x.3x.4x+4=?
= (1.2.3.4)(x.x.x.x)+4
=24x4+4
Đúng 0
Bình luận (0)
= (1.2.3.4)(x.x.x.x)+4
=24 x^4
Đúng 0
Bình luận (0)