Cho hình thang vuông có các cạnh đáy bằng 3 và 8. Tính hiệu các bình phương của hai đường chéo.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
một hình thang vuông có tổng hai đáy bằng a, hiệu hai day bằng b. tính hiệu các bình phương của hai đường chéo.
Giả sử ABCD là một hình thang vuông, góc A = góc D = 900 (ở đây mk chỉ xét 1 TH đáy nhỏ AB,đáy lớn CD,TH còn lại t.tự)
=>tam giác ABD và tam giác ADC vuông tại A và D
Xét tam giác ABD vuông tại A: \(BD^2=AB^2+AD^2\) (đ/l Pytago)
Xét tam giác ADC vuông tại D : \(AC^2=AD^2+CD^2\) (đ/l Pytago)
\(=>AC^2-BD^2=AD^2+CD^2-\left(AB^2+AD^2\right)=CD^2-AB^2=\left(CD-AB\right).\left(CD+AB\right)\)
Vì \(CD-AB=b;CD+AB=a\)
\(=>AC^2-BC^2=a.b\)
Vậy...........................
Kính chào thầy, cô và các bạn. Xin giải giúp em bài toán này :
Cho hình thang vuông có các cạnh đáy bằng 3cm và 8cm. Tính hiệu các bình phương của hai đường chéo?
Em xin trân trọng cảm ơn !
thui bn nghỉ học lun đi làm MC đủ sống rùi
ko bt thi nói ik.tr lời z đâu ko !!!
cho hình thang vuông có tổng 2 đáy bằng a hiệu 2 đáy bằng b tính hiệu các bình phương của 2 đường chéo
Kẻ đường cao thứ 2, kẻ 2 đường chéo rồi Py-ta-go
gọi hình thang vuông là ABCD
nên AB+CD=a
và DC-AB=b
ta có \(\Delta ADC\)vuông ở D
\(\Rightarrow\)\(AD^2+DC^2=AC^2\left(1\right)\)
Xét \(\Delta DAB\)vuông ở A
\(\Rightarrow DA^2+AB^2=DB^2\)
Từ (1) và (2) suy ra
\(AC^2-DB^2=\left(AD^2+DC^2\right)-\left(DA^2+AB^2\right)\)
\(=DC^2-AB^2\)
\(=\left(DC-AB\right)\times\left(DC+AB\right)\)
=b\(\times\)a
chứng minh rằng trong hình thang vuông, hiệu các bình phương hai đường chéo bằng hiệu các bình phương hai đáy
Cho hình thang \(ABCD\left(AB//CD\right)\)có hai đường chéo vuông góc với nhau.
a) Chứng minh tổng các bình phương của hai đáy bằng tổng các bình phương của hai cạnh bên.
b) Chứng minh tổng các bình phương của hai đường chéo bằng bình phương của tổng hai đáy.
c) Kẻ đường cao AH và đường trung bình MN của hình thanh ABCD. Biết BD=9cm, AC=12cm.
Tính diện tích tứ giác AMHN
Chứng minh rằng : Trong hình thang vuông , hiệu các bình phương hai đường chéo bằng hiệu các bình phương hai đáy
https://olm.vn/hoi-dap/question/655995.html
bạn vào đây tham khảo nha
Vì \(\Delta ADC\)vuông nên ta có :
Áp dụng định lí Py-ta-go :
\(AC^2=AD^2+DC^2\)(1)
Vì \(\Delta ABD\)vuông nên ta có :
Áp dụng định lí py-ta-go :
\(BD^2=AD^2+AB^2\)(2)
Từ (1) và (2)
\(\Rightarrow AC^2-BD^2=DC^2-AB^2\)
( đpcm)
Một hình thang vuông có tổng hai đáy bằng a, hiệu hai đáy bằng b. Tính hiệu các bình phương của hai đường chéo.
Mong các bác giúp đỡ!
Cho một hình thang vuông có tổng 2 đáy = a ,hiệu 2 đáy = b.Tính hiệu các bình phương của 2 đường chéo
Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6cm, cạnh bên AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh DC, CB và đường chéo DB.
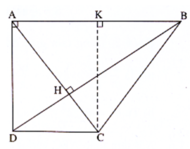
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
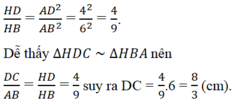
Kẻ đường cao CK của tam giác ABC, dễ thấy KB = AB – DC = 6 - 8/3 = 10/3.
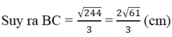
Tam giác vuông ABD có D B 2 = A B 2 + A D 2 = 6 2 + 4 2 = 52, từ đó DB = 52 = 2 13 (cm)