Trong tất cả n số tự nhiên khác nhau mà mỗi số đều có 7 chữ số được viết ra từ các chữ số 1;2;3;4;5;6;7 thì có k số chia hết cho 5 và m số chia hết cho 2.Hãy tính các số n;k;m
(giải dùng máy tính bỏ túi nha)
NL
Những câu hỏi liên quan
Từ bốn chữ số 2, 5, 7, 9. Viết được tất cả bao nhiêu số tự nhiên có bốn chữ số mà các chữ số đó đều khác nhau?
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
A
.
504
59049
B
.
7560
59049
C
.
1260
59049
D
.
12600...
Đọc tiếp
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
A . 504 59049
B . 7560 59049
C . 1260 59049
D . 12600 59049
Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: 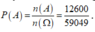
Đúng 0
Bình luận (0)
Từ tập hợp tất cả các số tự nhiên có 5 chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Tính xác suất để trong số tự nhiên lấy ra được chỉ có mặt 3 chữ số khác nhau.
từ bốn chữ số 3 ; 6 ; 7 ; 9 viết được tất cả bao nhiêu số tự nhiên có bốn chữ số mà các chữ số đó đều khác nhau ?
XÉT: hàng nghìn được 4 trường hợp.
hàng trăm được 3 trường hợp
hàng chục được 2 trường hợp
hàng đơn vị có 1 trường hợp
(các trường hpowj trong mỗi hàng không thể giống nhau vì 4 chữ số phải khcs nhau)
VẬY VIẾT ĐƯỢC TẤT CẢ 10 SỐ TỰ NHIÊN CÓ 4 C/S MÀ CÁC C/S ĐỀU KHÁC NHAU.
K MK NHA. CHÚC BN HỌC TỐT. ^_^
Đúng 0
Bình luận (0)
Số thứ 1 có 4 lựa chọn
Số thứ 2 có 3 lựa chọn
Số thứ 3 có 2 lựa chọn
Số thứ 4 có 1 lựa chọn
Suy ra có tất cả 1*2*3*4=24
đáp án:24
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Cho 4 chữ số: 0, 2, 3, 5. Hãy lập tất cả các số mà mỗi số có đủ 4 chữ số đã cho. Tính tổng.Bài 2: Cho 4 chữ số: 1, 3, 3, 4. Hãy lập tất cả các số có 4 chữ số mà mỗi số có đủ 4 chữ số đã cho. Tính tổng.Bài 3: Cho 5 chữ số: 0, 1, 3, 2, 4. Hãy lập tất cả các số có 5 chữ số mà mỗi số có đủ 5 chữ số đã cho. Tính tổng.Bài 4: Cho 5 chữ số 0, 1, 2, 3, 4.a, Có thể viết đượcbao nhiêu số có 4 chữ số khác nhau từ 5 chữ số đã cho? Trong các số viết được có bao nhiêu số chẵn?b, Tìm số chẵn lớn nhất, số...
Đọc tiếp
Bài 1: Cho 4 chữ số: 0, 2, 3, 5. Hãy lập tất cả các số mà mỗi số có đủ 4 chữ số đã cho. Tính tổng.
Bài 2: Cho 4 chữ số: 1, 3, 3, 4. Hãy lập tất cả các số có 4 chữ số mà mỗi số có đủ 4 chữ số đã cho. Tính tổng.
Bài 3: Cho 5 chữ số: 0, 1, 3, 2, 4. Hãy lập tất cả các số có 5 chữ số mà mỗi số có đủ 5 chữ số đã cho. Tính tổng.
Bài 4: Cho 5 chữ số 0, 1, 2, 3, 4.
a, Có thể viết đượcbao nhiêu số có 4 chữ số khác nhau từ 5 chữ số đã cho? Trong các số viết được có bao nhiêu số chẵn?
b, Tìm số chẵn lớn nhất, số lẻ nhỏ nhất có 4 chữ số khác nhau được viết từ 5 chữ số đã cho
Bài 5: Có thể viết được bao nhiêu số có 3 chữ số khác nhau, biết rằng:
a, Các chữ số của chúng đều là những số lẻ?
b, Các chữ số của chúng đều là những số chẵn?
Bài 6:
a, Tìm số tự nhiên nhỏ nhất có 5 chữ số được viết tữ 3 chữ số khác nhau.
b, Tìm số tự nhiên lớn nhất có 5 chữ số được viết từ 3 chữ số khác nhau.
Bài 7: Viết liên tiếp các số tự nhiên từ 1 đến 15 để được 1 số tự nhiên. Hãy xoá đi 10 chữ số vừa nhận được mà vẫn giữ nguyên thứ tự của các chữ số còn lại để được:
a, Số lớn nhất;
b, Số nhỏ nhất; Viết các số đó.
Bài 8: Viết liên tiếp 10 số chẵn khác 0 đầu tiên để được một số tự nhiên. Hãy xoá đi 10 chữ số của số vừa nhận được mà vẫn giữ nguyên thứ tự của các chữ số còn lại để được: a, Số chẵn lớn nhất; b, Số lẻ nhỏ nhất.
Các số là:
2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320
2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563
Đúng 0
Bình luận (0)
Tinh tong sai bet .phai la 64440.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Từ bốn chữ số 2;5;7;9 viết được tất cả bao nhiêu số tự nhiên có bốn chữ số mà các chữ số đó đều khác nhau?
· Có 4 cách chọn chữ số hàng nghìn ( chọn 2 hoặc 5 hoặc 7 hoặc 9)
· Sau khi chọn chữ số hàng nghìn thì còn 3 cách chọn chữ số hàng trăm.
· Sau khi chọn chữ số hàng nghìn và hàng trăm thì còn 2 cách chọn chữ số hàng chục.
· Cuối cùng chỉ còn 1 cách chọn chữ số hàng đơn vị.
Vậy ta viết được tất cả 4.3.2.1=24 (số).
Đúng 0
Bình luận (0)
Câu 1: Số a bằng 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11................được viết bởi các số tự nhiên liên tiếp từ 1. Chữ số 2010 từ trái sang phải của số a là chữ số nào?Câu 2: Số tự nhiên lớn nhất có các chữ số khác nhau mà tích các chữ số của nó bằng 840. Tìm số đó?Câu 3: Có tất cả bao nhiêu số có 3 chữ số khác nhau mà các số đó đều không chia hết cho 5?Câu 4:Số tự nhiên bé nhất có tổng các chữ số là 40 là số nào?Câu 5: Khoảng thời gian 6 giờ sáng nay đến bây giờ bằng 1/4 khoảng thời gian từ bây gi...
Đọc tiếp
Câu 1: Số a bằng 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11................được viết bởi các số tự nhiên liên tiếp từ 1. Chữ số 2010 từ trái sang phải của số a là chữ số nào?
Câu 2: Số tự nhiên lớn nhất có các chữ số khác nhau mà tích các chữ số của nó bằng 840. Tìm số đó?
Câu 3: Có tất cả bao nhiêu số có 3 chữ số khác nhau mà các số đó đều không chia hết cho 5?
Câu 4:Số tự nhiên bé nhất có tổng các chữ số là 40 là số nào?
Câu 5: Khoảng thời gian 6 giờ sáng nay đến bây giờ bằng 1/4 khoảng thời gian từ bây giờ đến 7 giờ sáng ngày mai. Hỏi bây giờ là mấy giờ?
Câu 6: Có tất cả bao nhiêu số có 2 chữ số mà mỗi số đó đều chia hết cho cả 2 và 3?
Cho bốn chữ số : 1 ; 2 ; 3 ; 4 .
Hãy viết tất cả các số tự nhiên khác nhau có bốn chữ số mà mỗi số đều có bốn chữ số trên
1234 , 1243 , 1342 , 1324 , 1432 , 1423
2341 , 2314 , 2413 , 2431 , 2134 , 2143
3124 , 3142 , 3241 , 3214 , 3412 , 3421
4321 , 4312 , 4231 , 4213 , 4132 , 4123
chuc ban hoc tot
Đúng 0
Bình luận (0)
Từ bốn chữ số 1; 2; 3; 4, ta viết được tất cả các số tự nhiên có bốn chữ số mà mỗi số đều có bốn chữ số trên là:
1234; 1243; 1324; 1342; 1423; 1432
2134; 2143; 2314; 2341; 2413; 2431
3124; 3142; 3214; 3241; 3412; 3421
4123; 4132; 4213; 4231; 4312; 4321
Chúc bạn học tốt
Đúng 0
Bình luận (0)
Các số đó là :
| 1234 | 1243 | 1324 | 1342 | 1423 | 1432 |
| 2134 | 2143 | 2314 | 2341 | 2431 | 2413 |
| 3124 | 3142 | 3214 | 3241 | 3421 | 3412 |
| 4123 | 4132 | 4213 | 4231 | 4321 | 4312 |
Đúng 0
Bình luận (0)
Từ bốn số 3; 6; 7; 9 viết được tất cả các số tự nhiên có ba chữ số mà các chữ số đó khác nhau
=> 367; 369; 376; 379; 396; 397. Như vậy ta có : mỗi một chữ số ta vt đc 6 số.
Từ ba chữ số trên, ta có thể lập đc :
4 x 6 = 24 ( số )
#Mạn
Đúng 0
Bình luận (0)


