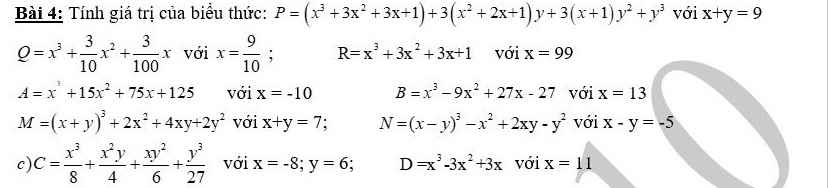
giúp mình câu Q,R,A,C
KL
Những câu hỏi liên quan
mình mình 
mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
ảnh kia nhiều người lắm like thế :)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn nội tiếp (O;R); ngoại tiếp (O:r); trực tâm H. Gọi k_a,k_b,k_c theo thứ tự là khoảng cách từ O đến BC, CA, AB. chứng minh:1.k_a+k_b+k_cR+r2.HA+HB+HC2(R+r)3.frac{a}{k_a}+frac{b}{k_b}+frac{c}{k_c}frac{abc}{4k_ak_bk_c}4.frac{a}{HA}+frac{b}{HB}+frac{c}{HC}frac{abc}{HA.HB.HC}các bạn giúp câu 2,3,4câu 1 mình tự làm được rồicảm ơn nhé
Đọc tiếp
cho tam giác ABC nhọn nội tiếp (O;R); ngoại tiếp (O':r); trực tâm H. Gọi \(k_a,k_b,k_c\) theo thứ tự là khoảng cách từ O đến BC, CA, AB. chứng minh:
1.\(k_a+k_b+k_c\)=R+r
2.HA+HB+HC=2(R+r)
3.\(\frac{a}{k_a}+\frac{b}{k_b}+\frac{c}{k_c}=\frac{abc}{4k_ak_bk_c}\)
4.\(\frac{a}{HA}+\frac{b}{HB}+\frac{c}{HC}=\frac{abc}{HA.HB.HC}\)
các bạn giúp câu 2,3,4
câu 1 mình tự làm được rồi
cảm ơn nhé
Xem chi tiết
Trên tia Mx xác định 2 điểm N và Q sao cho MN = 4cm, MQ = 8cm
a) Tính NQ
b) Điểm N có là trung điểm của đoạn thẳng MQ không?
c) điểm R là điểm nằm giữa 2 điểm M,N. Chứng tỏ RN = 1/2 (RQ - RM )
Mình làm được câu a,b rồi các bạn ráng giúp mình câu c nhé
( Do bạn đã làm câu a và b rồi, nên mình đi vào câu c luôn nha. )
Câu c: Giải:
Vì N là trung điểm của đoạn thẳng MQ
nên: MN + NQ = MQ và MN = NQ (1)
Ta có: RQ = RN + NQ (2)
RM = MN - RN (3)
Lấy (2) trừ (3) vế theo vế, ta có:
RQ - RM = ( RN + NQ ) - ( MN - RN )
RQ - RM = RN + NQ - MN + RN
RQ - RM = 2RN ( do NQ = MN nên NQ - MN = 0 )
RN = ( RQ - RM ) : 2
Vậy: điều đó chứng tỏ rằng RN = 1/2 ( RQ - RM )
Cho đường tròn (O;R) có hai đường kính AB và CD vuông góc với nhau. Gọi M là trung điểm của OB, tia CM cắt đường tròn (O;R) tại Ea) chứng minh tứ giác OMED nội tiếp.Xác địng tâm K và vẽ đường tròn đó b) Tiếp tuyến tại E của đường tròn (O;R) cắt AB tại F, cắt đường tròn tâm K tại Q. chứng minh FMFEc) chứng minh tứ giác COQE là hình thang, tính diện tích hình thang đó theo RGiải giúp mình câu b) c) nha câu a) mình làm được
Đọc tiếp
Cho đường tròn (O;R) có hai đường kính AB và CD vuông góc với nhau. Gọi M là trung điểm của OB, tia CM cắt đường tròn (O;R) tại E
a) chứng minh tứ giác OMED nội tiếp.Xác địng tâm K và vẽ đường tròn đó
b) Tiếp tuyến tại E của đường tròn (O;R) cắt AB tại F, cắt đường tròn tâm K tại Q. chứng minh FM=FE
c) chứng minh tứ giác COQE là hình thang, tính diện tích hình thang đó theo R
Giải giúp mình câu b) c) nha câu a) mình làm được
Cho (O;R) và điểm A có OA = 2R. Kẻ tiếp tuyến AB,AC và cát tuyến AMN với đường tròn. Gọi I là trung điểm của MN. BC cắt OA và MB tại H và K.
a) OA vuông góc với BC
b) Tính OM theo R
c) \(\Delta ABC\)đều
d) AI . AK = AO . AH
Giúp mình câu b,c,d với ạ =)) mình cần gấp
Mình không hiểu ý câu b. Chẳng lẽ đơn giản là \(OM=R\)? Đề cho vậy sao được?
Câu c: \(\sin\widehat{BAO}=\frac{OB}{OA}=\frac{1}{2}\Rightarrow\widehat{BAO}=30^o\Rightarrow\widehat{BAC}=60^o\)
Vậy tam giác \(ABC\) vừa có vừa có góc 60 độ nên nó đều.
Câu d: Tam giác \(AIO\) và \(AHK\) đồng dạng nha bạn.
Đúng 0
Bình luận (0)
câu b tức là tính OM theo bán kính R đó bạn. Nghĩa là gắn OM vào những cái số đo liên quan đến R để tính...
Đúng 0
Bình luận (0)
Ý mình là đơn giản \(OM=R\) thôi sao? Vì \(M\) nằm trên đường tròn mà! Đề cho hiển nhiên thế thì cho làm gì?
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a, b, c là các số tự nhiên khác 0 sao cho p = ab + c; q = bc + a; r = ca + b là các số
nguyên tố. Chứng minh rằng hai trong các số p, q, r phải bằng nhau.
Bài này khó quá giúp mình luôn nha mình là học sinh mới đăng kí.
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\)và \(a+b+c\ne0\)
tìm\(P=\frac{a^{10}.b^5.c^{2019}}{b^{2018}}\)
giúp mình với mai mình đi học r
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{b}=1\\\frac{b}{c}=1\\\frac{c}{a}=1\end{cases}}\Rightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Rightarrow}a=b=c\)
Thay a = b = c vào P
\(\Rightarrow P=\frac{b^{10}.b^5.b^{2019}}{b^{2018}}=\frac{b^{2034}}{b^{2018}}=b^{16}\)
GIÚP MÌNH VỚI M.N!!!
Cho tam giác ABC vuông tại A ngoại tiếp đường tròn (O;r). Đặt AB = c, BC = a, CA = b và \(2p=a+b+c\)
a. chứng minh: \(S_{ABC}=p.r\)
b) Đường cao AH = h. Chứng minh: \(2r< h\le\left(\sqrt{2}+1\right)\) ( cần lắm một câu trả lời)