a, Xét \(\Delta BAD\)và \(\Delta CAE\), có:

\(\widehat{AEC}=\widehat{ADB}=90^o\)(gt)

\(\widehat{A}\)là góc chung (gt)

\(\Rightarrow\) \(\Delta BAD\)đồng dạng \(\Delta CAE\)(trường hợp đồng dạng thứ 3)

b, Xét \(\Delta BHE\)và \(\Delta CHD\), có:

\(\widehat{BHE}=\widehat{CHD}\)(đối đỉnh)

\(\widehat{BEH}=\widehat{CDH}=90^o\)(vì ​\(\widehat{BEC}=\widehat{CDB}=90^o\), gt)

\(\Rightarrow\Delta BEC\)đồng dạng với \(\Delta CHD\)(trường hợp đồng dạng thứ ba)

\(\Rightarrow\frac{HB}{HE}=\frac{HC}{HD}\Leftrightarrow HB.HD=HC.HE\left(đpcm\right)\)

c, Xét \(\Delta BHC\)và \(\Delta DHE\), có:

\(\widehat{BHC}=\widehat{DHE}\)(đối đỉnh)

\(\frac{HB}{HE}=\frac{HC}{HD}\)(chúng minh trên)

\(\Rightarrow\Delta BHC\)đồng dạng với \(\Delta DHE\)(trường hợp đồng dạng thứ hai)

d, Xét \(\Delta ADB\)và \(\Delta BEH\), có:

\(\widehat{B}\)là góc chung (gt)

\(\widehat{ADB}=\widehat{BEC}=90^o\)(gt)

\(\Rightarrow\Delta ADB\)đồng dạng với \(\Delta BEH\)(trường hợp đồng dạng thứ ba)

Mà: \(\Delta BEH\)đồng dạng với \(\Delta CDH\)(c/m câu b)

\(\Rightarrow\Delta ADB\)đồng dạng với \(\Delta CDH\)(theo tính chất bắc cầu)

\(\Rightarrow\frac{DH}{DE}=\frac{DC}{DB}\Leftrightarrow DH.DB=DA.DC\left(đpcm\right)\)

Chúc bạn học tốt!

H là giao điểm của BD và CE à ? Trong đề không có cho dữ kiện này 

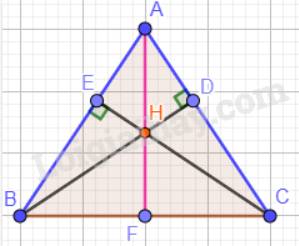
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).

Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ  - 70^\circ  - 70^\circ  = 40^\circ \).

b) Xét tam giác vuông ADB và tam giác vuông AEC có:

     AB = AC (tam giác ABC cân);

     \(\widehat A\) chung.

Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).

c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.

Xét hai tam giác vuông AFB và AFC có:

     AB = AC (tam giác ABC cân);

     AF chung.

Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).

Vậy tia AH là tia phân giác của góc BAC.

Góc ABD= góc ACE (hai góc có cạnh tương ứng vuông góc cùng nhọn)

Suy ra góc ABI= góc KCA (cùng bù vk hai góc bằng nhau)

Tam giác ABI= tam giác KCA (c-g-c)

Suy ra AI=AK (1) và góc BAI=góc K

Xét tam giác EAK vuông tại E có góc BAK+góc BAI=90^o

Hay góc IAK=90⁰ (2)

Từ (1) và (2) suy ra tam giác AIK vuông cân tại A  (đpcm)

a, Xét tam giác ABD và tam giác ACE

    +, Chung​ góc A​

    +, Góc ADB = góc AEC( = 90​ độ)

Suy ra tam giác ABD đồng dạng với tam giác ACE