Dựa vào công thức tính diện tích của đa giác đều để chứng minh công thức tính diện tích hình tròn
DT
Những câu hỏi liên quan
Chứng minh công thức tính diện tích tổng quát của đa giác đều có số cạnh là n. Từ đó suy ra công thức tính diện tích hình tròn.
Hãy dựa vào công thức tính diện tích hình thang để tính diện tích hình bình hành.
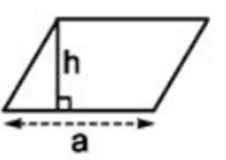
Hình bình hành là hình thang có hai đáy bằng nhau
⇒ Hình bình hành có cạnh đáy a và chiều cao h là:
S = 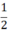 h(a + a) =
h(a + a) = 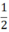 h.2a = a.h
h.2a = a.h
Đúng 0
Bình luận (0)
Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.
Đọc tiếp
Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.
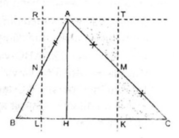
Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
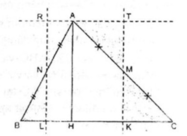
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC
Đúng 0
Bình luận (0)
Ba tính chất của diện tích đa giác đã được vận dụng như thế nào khi chứng minh công thức tính diện tích tam giác vuông?
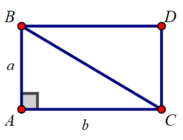
Muốn tính diện tích tam giác vuông ABC, ta dựng hình chữ nhật ABDC như trên
- ∆ABC = ∆DCB (hai cạnh góc vuông)
⇒SABC = SDCB (theo tính chất 1 diện tích đa giác) (1)
Đường chéo BC chia hình chữ nhật ABDC thành 2 phần là ∆ABC và ∆DCB
⇒SABDC = SABC + SDCB (theo tính chất 2 diện tích đa giác) (2)
Từ (1) và (2) ⇒ SABDC = 2SABC ⇒ SABC = 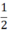 SABDC
SABDC
- ABDC là hình chữ nhật ⇒ SABDC = a.b
⇒ SABC = 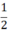 SABDC =
SABDC = 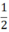 ab
ab
Đúng 0
Bình luận (0)
* ToánCông thức tính diện tích hcnCông thức tính diện tích hình vuôngCông thức tích diện tích, chu vi của tam giácCông thức tính diện tích hình thoi* Ngữ văn:Viết 1 đoạn văn từ 5-7 câu nói về số phận người phụ nữ trước Cách mạng Tháng Tám qua một số tác phẩm đã học ở lớp 8(Các bạn có thể dựa vào bài Trong lòng mẹ, Tức nước vỡ bờ)
Đọc tiếp
* Toán
Công thức tính diện tích hcn
Công thức tính diện tích hình vuông
Công thức tích diện tích, chu vi của tam giác
Công thức tính diện tích hình thoi
* Ngữ văn:
Viết 1 đoạn văn từ 5-7 câu nói về số phận người phụ nữ trước Cách mạng Tháng Tám qua một số tác phẩm đã học ở lớp 8
(Các bạn có thể dựa vào bài ''Trong lòng mẹ'', ''Tức nước vỡ bờ'')
Trl :
* Toán :
Công thức tính diện tích Hình chữ nhật
Diện tích: S = a x b.
Công thức tính diện tích Hình vuông
S = a x a.
Biết DT tìm cạnh bằng cách nhẩm.
Công thức tính diện tích Hình tam giác
S = (a x h) : 2
Trong đó:
a là cạnh đáyh : chiều caoChiều cao: h = (S x 2) : a
Cạnh đáy: a = (S x 2) : h
Công thức tính chu vi Hình tam giác
P = a + b + c
Trong đó:
a là cạnh thứ nhấtb là cạnh thứ haic là cạnh thứ baCông thức tính diện tích Hình thoi
S = (a x b) : 2
Trong đó: a và b là số đo độ dài hai đường chéo.
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
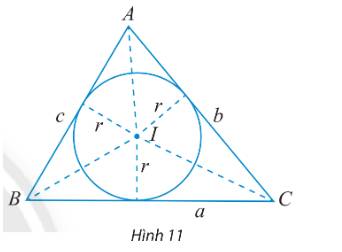
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)
Đúng 0
Bình luận (0)
Viết các công thức tính chu vi , diện tích của hình chữ nhật , hình vuông , hình tam giác , hình bình hành , hình thoi , hình thang , hình tròn . Công thức tính Thể tích hình lập phương , hình hộp chữ nhật . Công thức tính Chiều cao hình tam giác , hình thang , hình bình hành . Công thức tính Đáy hình tam giác , hình thang , hình bình hành . Công thức tính Đường kính , bán kính hình tròn .
HÌNH CHỮ NHẬT
Chu vi: P = (a + b) x 2 (P: chu vi)Diện tích: S = a x b (S: diện tích)HÌNH VUÔNG:
Chu vi: P = a x 4 (P: chu vi)Diện tích: S = a x a (S: diện tích)HÌNH TAM GIÁC:
Chu vi: P = a + b + c (a: cạnh thứ nhất; b: cạnh thứ hai; c: cạnh thứ ba)Diện tích: S = (a x h) : 2 (a: cạnh đáy)Chiều cao: h = (S x 2) : a (h: chiều cao)Cạnh đáy: a = (S x 2) : hHÌNH BÌNH HÀNH:
Chu vi: P = (a + b) x 2 (a: độ dài đáy)Diện tích: S = a x h (b: cạnh bên)Diện tích: S = a x h (h: chiều cao)Độ dài đáy: a = S : hChiều cao: h = S : aDiện tích: S = (m x n) : 2 (m: đường chéo thứ nhất)Tích 2 đường chéo: (m x n) = S x 2 (n: đường chéo thứ nhất)HÌNH THANGDiện tích: S = (a + b) x h : 2 (a & b: cạnh đáy)Chiều cao: h = (S x 2) : a (h: chiều cao)Cạnh đáy: a = (S x 2) : hHÌNH TRÒN:
Bán kính hình tròn: r = d : 2 hoặc r = C : 2 : 3,14Đường kính hình tròn: d = r x 2 hoặc d = C : 3,14Chu vi hình tròn: C = r x 2 x 3,14 hoặc C = d x 3,14Diện tích hình tròn: C = r x r x 3,14Diện tích xung quanh: Sxq = (a x a) x 4Cạnh: (a x a) = Sxq : 4Diện tích toàn phần: Stp = (a x a) x 6Cạnh: (a x a) = Stp : 6Diện tích xung quanh: Sxq = Pđáy x hChu vi đáy: Pđáy = Sxq : hChiều cao: h = Pđáy x Sxq
Đúng 5
Bình luận (0)
;uodfrwEY{{{{{{{{{Ơ3tuj80g
Xem thêm câu trả lời
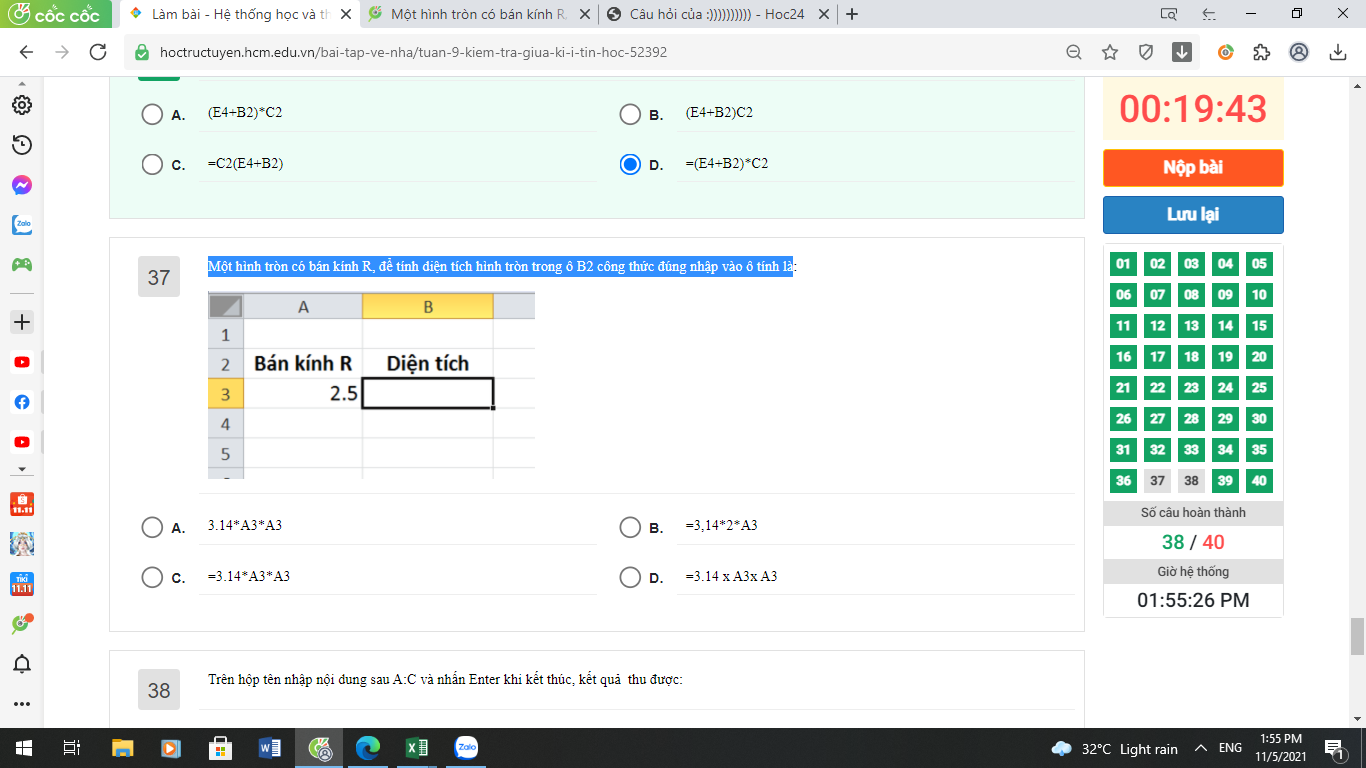
Một hình tròn có bán kính R, để tính diện tích hình tròn trong ô B2 công thức đúng nhập vào ô tính là
1. Hãy phát biểu bằng lời:a) Công thức tính diện tích xung quanh của hình trụ.b) Công thức tính thể tích của hình trụ.c) Công thức tính diện tích xung quanh của hình nón.d) Công thức tính thể tích của hình nón.e) Công thức tính diện tích của mặt cầu.f) Công thức tính thể tích của hình cầu.
Đọc tiếp
1. Hãy phát biểu bằng lời:
a) Công thức tính diện tích xung quanh của hình trụ.
b) Công thức tính thể tích của hình trụ.
c) Công thức tính diện tích xung quanh của hình nón.
d) Công thức tính thể tích của hình nón.
e) Công thức tính diện tích của mặt cầu.
f) Công thức tính thể tích của hình cầu.
a) Diện tích xung quanh hình lăng trụ thì bằng chu vi đường tròn đáy nhân với chiều cao.
b) Thể tích hình trụ thì bằng tích của diện tích hình tròn đáy nhân với đường cao.
c) Diện tích xung quanh hình nón thì bằng 1/2 tích của chu vi đường tròn đáy với đường sinh.
d) Thể tích hình nón bằng 1/3 tích của diện tích hình tròn đáy với chiều cao.
e) Diện tích mặt cầu thì bằng 4 lần diện tích hình tròn lớn.
f) Thể tích hình cầu thì bằng 4/3 tích của diện tích hình tròn lớn với bán kính.
Đúng 0
Bình luận (0)

