Tìm các số nguyên a, b sao cho ab-3b=4b-5a
Giúp mình nhé
Tìm các số nguyên a, b sao cho ab-3b=4b-5a
Tìm các số nguyên a , b sao cho ab - 3b = 4b - 5a ( b >= 3 )
1) Tìm số nguyên tố abcd (gạch đầu) sao cho ab , cd là số nguyên tố và b2= cd + b-c ( tất cả đều có gạch đầu nhé! )
2) Tìm các số nguyên tố a,b,c sao cho :
a) 3a + 4b +6c = 68 ( không gạch đầu nhé !)
b) ab + 1 =c
Tìm các số nguyên a, b sao cho: ab+11=2a+3b
Lời giải:
$ab+11=2a+3b$
$ab-2a-3b+11=0$
$a(b-2)-3(b-2)+5=0$
$(a-3)(b-2)=-5$
Vì $a,b$ là số nguyên nên $a-3, b-2$ là số nguyên. Ta có bảng sau: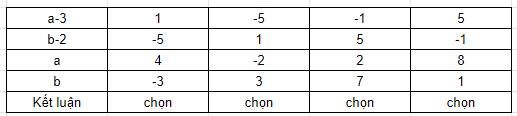
Tìm các số nguyên a, b sao cho: ab + 11 = 2a + 3b
Tìm các số nguyên a,b sao cho ab-2b=4b-3a
Giúp mình bài này với [ nhớ chi tiết nhé ]
Tìm các số nguyên tố a , b , c
a + 3b = 24
2a + 3b = 78
[ Ai làm đúng mình tick cho ]
Các bạn trình bày lời giải hoặc gợi ý nhé, mình cần gấp! Cảm ơn các bạn nhiều!
1. Tìm các số tự nhiên a, b, c sao cho a^2 - b, b^2 - c, c^2 - a đều là các số chính phương.
2. Cho các số nguyên dương x, y thỏa mãn điều kiện x^2 + y^2 + 2x(y+1) - 2y là số chính phương. CMR: x = y
3. Tìm số nguyên n thỏa mãn (n^2 - 5)(n + 2) là số chính phương
4. Tìm các số tự nhiên a, b thỏa mãn a^2 + 3b; b^2 + 3a đều là các số chính phương
5. Cho các số nguyên a, b, c thỏa mãn a^2 + b^2 + c^2 = 2(ab + bc + ca). CMR ab + bc + ca, ab, bc, ca đều là các số chính phương.
thtfgfgfghggggggggggggggggggggg
Tìm a,b,c thỏa mãn :
a. 3a = 4b , 2b = 5c và 2^2 + b^2 + c^2 = 661
b. 2a = 3b = 4c và 3a + 4b - c = 72
Các bạn làm nhanh giúp mình nhé chiều nay mình phải nộp rồi . Cảm ơn các bạn rất nhiều ;))
Ta có \(\hept{\begin{cases}3a=4b\\2b=5c\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{b}{3}=\frac{a}{4}\\\frac{b}{5}=\frac{c}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{b}{15}=\frac{a}{20}\\\frac{b}{15}=\frac{c}{6}\end{cases}}\Leftrightarrow\frac{a}{20}=\frac{b}{15}=\frac{c}{6}\)
Đặt \(\frac{a}{20}=\frac{b}{15}=\frac{c}{6}=k\Leftrightarrow\hept{\begin{cases}a=20k\\b=15k\\c=6k\end{cases}}\)
Khi đó a2 + b2 + c2 = 661
<=> (20k)2 + (15k)2 + (6k)2 = 661
<=> 661k2 = 661
<=> k2 = 1
<=> k = \(\pm1\)
Khi k = 1 => a = 20 ; b = 15 ; c = 6
Khi k = -1 => a = -20 ; b = - 15 ; c = -6
Ta có \(2a=3b=4c\Leftrightarrow\frac{2a}{12}=\frac{3b}{12}=\frac{4c}{12}\Leftrightarrow\frac{a}{6}=\frac{b}{4}=\frac{c}{3}\)
Áp dụng dãy tỉ số bằng nhau ta có :
\(\frac{a}{6}=\frac{b}{4}=\frac{c}{3}=\frac{3a}{18}=\frac{4b}{16}=\frac{3a+4b-c}{18+16-3}=\frac{72}{31}\)
=> \(\hept{\begin{cases}a=\frac{432}{31}\\b=\frac{288}{31}\\c=\frac{216}{31}\end{cases}}\)