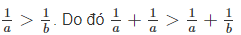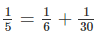Có bao nhiêu cách viết p/s 1/5 dưới dạng tổng của 2 p/s 1/a + 1/b với 0<a<b
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NP
Những câu hỏi liên quan
có bao nhiêu cách viết p/s 1/5 dưới dạng tổng của 2 p/s ;1/a va1/b với 0<a<b ?
cac ban giai ho minh nhe.giai chi tiet minh cho ****
Đúng 0
Bình luận (0)
có bao nhiêu cách viết p/s 1/5 dưới dạng 2 p/s 1/a + 1/b với 0<a<b ???
CÓ BAO NHIÊU CÁCH VIẾT 1/5 DƯỚI DẠNG TỔNG CỦA 2 PHÂN SỐ 1/A +1/B VỚI 0<A<B
có bao nhiêu cách viết 1/5 dưới dạng tổng của hai phân số 1/a + 1/b với 0< a <b ?
Có bao nhiêu cách viết phân số 1/5 dưới dạng tổng của hai phân số 1/a + 1/b với 0<a<b ? giải thích cụ thể
vì 1/a + 1/b = 1/5 nên 1/a < 1/5 => a >5 (1)
ta có: 0 < a < b nên 1/a > 1/b. do đó 1/a + 1/a > 1/a + 1/b
hay 2/a > 1/5 = 2/10
=> a < 10 (2)
từ (1) và (2) => a thuộc ( 6;7;8;9 )
nếu a = 6 thì 1/b = 1/5 - 1/6 = 1/30 nên b = 30
nếu a = 7 thì 1/b = 1/5 - 1/7 = 2/35 => b = 17,5 (loại)
nếu a = 8 thì 1/b = 1/5 - 1/8 = 3/40 => b = 13,3 (loại)
nếu a = 9 thì 1/b = 1/5 - 1/9 = 4/45 => b = 11,25 (loại)
vậy có 1 cách viết đó là 1/6 + 1/30 = 1/5
cái này mk vừa chữa sáng hôm qua trên lớp xong nên chắc chắn đúng đó k nha
Đúng 1
Bình luận (0)
Có bao nhiêu cách viết phân số 1/5 dưới dạng tổng của hai phân số 1 a + 1 b với 0 < a < b ?
Vì 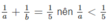 Suy ra a > 5 (1)
Suy ra a > 5 (1)
Ta lại có 0 < a < b nên 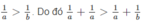
Hay 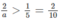 , suy ra a < 10 (2)
, suy ra a < 10 (2)
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì 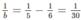 nên b = 30
nên b = 30
Nếu a = 7 thì 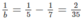 suy ra b = 17,5 (loại)
suy ra b = 17,5 (loại)
Nếu a = 8 thì 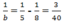 suy ra b ≈ 13,3 (loại)
suy ra b ≈ 13,3 (loại)
Nếu a = 9 thì 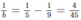 suy ra b = 11,25 (loại)
suy ra b = 11,25 (loại)
Vậy chỉ có một cách viết là 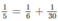
Đúng 0
Bình luận (0)
có bao nhiêu cách viết phân số\(\frac{1}{5}\)dưới dạng tổng của 2 phân số \(\frac{1}{a}+\frac{1}{b}\)với 0<a<b
các ước của 5 là:
1.5 và 5.1
số 1 bằng tổng của các số:1+0
vậy ta có các cặp phân số:
(1/5+1/1)+(1/1+1/5)
vậy ta có 2 cách viết phân số
Đúng 0
Bình luận (0)
Có bao nhiêu cách viết 1/5 dưới dạng tổng của hai ps 1/a + 1/b với 0<a<b?
Gíup mk đi!!! Mai kiểm tra rùi!!!!![]()
theo bài ra ,ta có:
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{5}\)
vì 0<a<b nên \(\frac{1}{a}>\frac{1}{b}\)
=> \(\frac{1}{a}+\frac{1}{a}>\frac{1}{a}+\frac{1}{b}\)
hay \(\frac{2}{a}>\frac{1}{5}\)
\(\frac{2}{a}>\frac{2}{10}\)
=>\(a< 10\) (1)
ta lại có: \(\frac{1}{a}< \frac{1}{5}\)
=>\(a>5\) (2)
từ (1) và (2) =>\(5< a< 10\)
=>\(a\in\left\{6;7;8;9\right\}\)
+) nếu a=6 thì \(\frac{1}{6}+\frac{1}{b}=\frac{1}{5}\)
\(\frac{1}{b}=\frac{1}{5}-\frac{1}{6}=\frac{1}{30}\)
=>\(b=30\)
+) nếu a=7 thì \(\frac{1}{7}+\frac{1}{b}=\frac{1}{5}\)
\(\frac{1}{b}=\frac{1}{5}-\frac{1}{7}=\frac{2}{35}\left(loai\right)\)
+) nếu a=8 thì \(\frac{1}{8}+\frac{1}{b}=\frac{1}{5}\)
\(\frac{1}{b}=\frac{1}{5}-\frac{1}{8}=\frac{3}{40}\left(loai\right)\)
+) nếu a=9 thì \(\frac{1}{9}+\frac{1}{b}=\frac{1}{5}\)
\(\frac{1}{b}=\frac{1}{5}-\frac{1}{9}=\frac{4}{45}\left(loai\right)\)
vậy có 1 cách viết \(\frac{1}{5}\) dưới dạng tổng \(\frac{1}{a}+\frac{1}{b}\) với \(0< a< b\) là \(\frac{1}{6}+\frac{1}{30}\)
Đúng 0
Bình luận (0)
Có bao nhiêu cách viết phân số \(\dfrac{1}{5}\) dưới dạng tổng của hai phân số \(\dfrac{1}{a}+\dfrac{1}{b}\) với \(0< a< b\) ?
Giải:
Ta có:
Do \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{a}< \dfrac{1}{5}\Leftrightarrow a>5\left(1\right)\)
Ta lại có:
\(0< a< b\Leftrightarrow\dfrac{1}{a}>\dfrac{1}{b}\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{a}>\dfrac{1}{a}+\dfrac{1}{b}\)
Hay \(\dfrac{2}{a}>\dfrac{1}{5}\Leftrightarrow\dfrac{2}{a}>\dfrac{2}{10}\Leftrightarrow a< 10\left(2\right)\)
Kết hợp \(\left(1\right)\) và \(\left(2\right)\Leftrightarrow a\in\left\{6;7;8;9\right\}\)
- Với \(a=6\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{1}{30}\Leftrightarrow b=30\)
- Với \(a=7\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{7}=\dfrac{2}{35}\Leftrightarrow b=17,5\) (loại)
- Với \(a=8\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{8}=\dfrac{3}{40}\Leftrightarrow b\approx13,3\) (loại)
- Với \(a=9\) thì \(\dfrac{1}{b}=\dfrac{1}{5}-\dfrac{1}{9}=\dfrac{4}{45}\Leftrightarrow b=11,25\) (loại)
Vậy chỉ có 1 cách viết là \(\dfrac{1}{5}=\dfrac{1}{6}+\dfrac{1}{30}\)
Đúng 0
Bình luận (0)
Vì 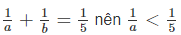
Ta lại có 0 < a < b nên
Hay 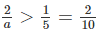
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì 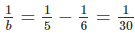
Nếu a = 7 thì 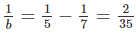
Nếu a = 8 thì 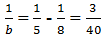
Nếu a = 9 thì 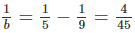
Vậy chỉ có một cách viết là
Đúng 0
Bình luận (0)
Vì 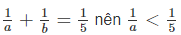
Ta lại có 0 < a < b nên
Hay 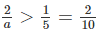
Từ (1) và (2) ta có a ∈ {6;7;8;9}
Nếu a = 6 thì 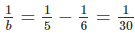
Nếu a = 7 thì 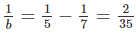
Nếu a = 8 thì 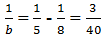
Nếu a = 9 thì 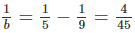
Vậy chỉ có một cách viết là
Đúng 0
Bình luận (0)