Lý thuyết cộng, trừ đa thức một biến.
NN
Những câu hỏi liên quan
Lý thuyết về cộng, trừ đa thức
1. Cộng đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
- Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng (nếu có).
2. Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực iện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng (nếu có).
Đúng 0
Bình luận (0)
1. Cộng đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
- Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng (nếu có).
2. Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực iện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng (nếu có).
Đúng 0
Bình luận (0)
1. Cộng đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
- Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng (nếu có).
2. Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực iện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng (nếu có).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Lý thuyết về nghiệm của đa thức một biến.
1. Nghiệm của đa thức một biến
Cho đa thức P(x)
Nếu tại x = a đa thức P(x) có giá trị bằng 0 thì ta nói a là một nghiệm của đa thức P(x).
2. Số nghiệm của đa thức một biến
Một đa thức (khác đa thức không) có thể có 1, 2, 3, ..., n nghiệm hoặc không có nghiệm nào.
Tổng quát: Số nghiệm của một đa thức (khác đa thức 0) không vượt qua bậc của nó.
Đúng 0
Bình luận (0)
cho tôi vài cái phép cộng trừ đa thức một biến tôi tự tập tính
1. Cho đa thức sau: \(A=7x^3-5x+6+2x^4\). Tìm các đa thức B, C sao cho:
\(A+B=6x^5+3-7x+6x^3\)
\(A-C=2x^4\)
2. Tìm tổng các đa thức sau:
\(a,3x^4+2x+6x^2-2x-1\)
\(b,-5x^4-3x^2+4x^3-2x-1\)
\(c,-x^5+3x^2-1\)
3. Tìm hiệu các đa thức sau:
\(a,2x^3-x^2+1,5\)
\(b,4x^6-x^5+3x-2\)
\(c,-6x^3-3x+x^2-4\)
Đúng 3
Bình luận (0)
Giúp giảng cho em về cách đổi dấu trong cộng trừ đa thức và đa thức một biến
trước các hạng tử có dấu gì thì đó chính là dấu của hạng từ
nếu hạng tử đầu tiên của đa thức không có dấu đằng trước, ta ngầm hiểu hạng tử đó mang dấu dương
quy tắc đổi dấu: khi cộng 2 đa thức thì giữ nguyên dấu các hạng tử của cả 2 đa thức và thực hiện cộng các đa thức cùng phần biến
khi trừ 2 đa thức thì giữ nguyên dấu các hạng tử của đa thức bị trừ, còn lại đổi dấu tất cả các hạng tử của đa thức trừ sau khi bỏ dấu ngoặc
thế này được chưa bạn![]()
![]()
![]()
Đúng 1
Bình luận (0)
Một số tình huống trong cuộc sống dẫn đến việc cộng, trừ hai đa thức một biến, chẳng hạn, ta phải tính tổng diện tích các mặt của hình hộp chữ nhật (Hình 2) có độ dài hai cạnh đáy là x (m), 2x (m) và chiều cao là 2 (m).Phép cộng, phép trừ hai đa thức một biến được thực hiện như thế nào?
Đọc tiếp
Một số tình huống trong cuộc sống dẫn đến việc cộng, trừ hai đa thức một biến, chẳng hạn, ta phải tính tổng diện tích các mặt của hình hộp chữ nhật (Hình 2) có độ dài hai cạnh đáy là x (m), 2x (m) và chiều cao là 2 (m).
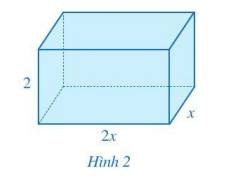
Phép cộng, phép trừ hai đa thức một biến được thực hiện như thế nào?
a) Cộng hai đa thức:
Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
- Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết tổng hai đơn thức theo hàng ngang;
- Nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
b) Trừ hai đa thức:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Đúng 0
Bình luận (0)
ưu điểm và nhược điểm của hai cách cộng trừ đa thức một biến là gì?
Câu 1:Thế nào là đơn thức,bậc của đơn thức?Nêu quy tắc nhân 2 đơn thức.Câu 2:Thế nào là 2 đơn thức đồng dạng?Nêu quy tắc cộng trừ 2 đơn thức đồng dạng.Câu 3:Thế nào là đa thức,bậc của đa thức?nêu cách cộng trừ đa thức 1 biến.Câu 4:Thế nào là nghiệm của đa thức 1 biến?Cách tìm nghiệm của đa thức 1 biến.Câu 5:Phát biểm các trường hợp bằng nhau của 2 tam giác.Các trường hợp bằng nhau của 2 tam giác vuông.
Đọc tiếp
Câu 1:Thế nào là đơn thức,bậc của đơn thức?Nêu quy tắc nhân 2 đơn thức.
Câu 2:Thế nào là 2 đơn thức đồng dạng?Nêu quy tắc cộng trừ 2 đơn thức đồng dạng.
Câu 3:Thế nào là đa thức,bậc của đa thức?nêu cách cộng trừ đa thức 1 biến.
Câu 4:Thế nào là nghiệm của đa thức 1 biến?Cách tìm nghiệm của đa thức 1 biến.
Câu 5:Phát biểm các trường hợp bằng nhau của 2 tam giác.Các trường hợp bằng nhau của 2 tam giác vuông.
Nhưng mình mất sách rùi!Bạn trả lời hộ mình đi!
Đúng 0
Bình luận (0)
các bạn có thể cho mình biết chi tiết cách cộng trừ đa thức một biến được không? Mk học rồi nhưng hơi mơ hồ phần này
cách 1 cộng theo hàng ngang (cái này dễ nên bạn tự làm nhé)
cách 2 cộng theo hàng dọc sắp xếp theo lũy thừa giảm dần của biến rồi cộng trừ như cộng trừ số số hàng
Đúng 0
Bình luận (0)
Cách 1 : cộng theo hàng ngang
Cách 2 : cộng theo hàng dọc ( đa số sử dụng cách này )
Đúng 0
Bình luận (0)
Theo quy tắc cộng, trừ đa thức (coi i là biến), hãy tính:
(3 + 2i) + (5 + 8i);
(7 + 5i) – (4 + 3i);
(3 + 2i) + (5 + 8i) = (3 + 5) + (2 + 8)i = 8 + 10i.
(7 + 5i) – (4 + 3i) = (7 – 4) + (5 – 3)i = 3 + 2i.
Đúng 0
Bình luận (0)


