Cho 🔺ABC vuông ở A ,AB=16cm, AC=30cm. Tính tỏngTổng GA+GB+GC, biết G là trọng tâm của 🔺ABC.
KR
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Có AB=16cm, AC=30cm, G là trọng tâm của tam giác ABC. Tính GA+GB+GC?
\(Cho\Delta ABC\)vuông tại A, có AB =12cm , AC= 16cm và trọng tâm G. Tính tổng GA + GB + GC.
Ta lần lượt có:
Trong \(\Delta ABC\)vuông tại A, suy ra:\(BC^2=AB^2+AC^2=12^2+16^2=400\Leftrightarrow BC=20cm.\)
Ta có:
\(GA=\frac{2}{3}AM=\frac{2}{3}.\frac{1}{2}BC=\frac{1}{3}.20=\frac{20}{3}cm.\)
Trong \(\Delta ABN\)vuông tại A, suy ra:\(BN^2=AB^2+AN^2=12^2+8^2=208\Leftrightarrow BN=\sqrt{208}\left(cm\right)\)
Khi đó:
\(GB=\frac{2}{3}BN=\frac{2}{3}\sqrt{208}=\frac{2\sqrt{208}}{3}=\frac{8}{3}\sqrt{13}\left(cm\right)\)
Trong \(\Delta ACP\)vuông tại A, suy ra:\(CP^2=AC^2+AP^2=16^2+6^2=292\Leftrightarrow CP=\sqrt{292}\left(cm\right)\)
Khi đó:
\(GC=\frac{2}{3}CP=\frac{2}{3}\sqrt{292}=\frac{2\sqrt{292}}{3}=\frac{4}{3}\sqrt{73}cm.\)
Suy ra:
\(GA+GB+GC=\frac{20}{3}+\frac{8}{3}\sqrt{13}+\frac{4}{3}\sqrt{73}=\frac{4}{3}\left(5+2\sqrt{13}+\sqrt{73}\right)\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB a; BC 2a và G là trọng tâm. Tính giá trị của biểu thức
G
A
→
.
G
B
→
+
G
B
→
.
G
C
→
+
G
C
→
....
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.
Tính giá trị của biểu thức G A → . G B → + G B → . G C → + G C → . G A
A. -3a2
B. -2a2
C. -4 a2/3
D. 2a2
Chọn C.
Vì ![]() nên
nên
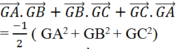
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
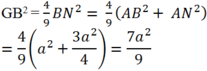
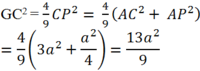
Suy ra
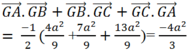
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm. Trọng tâm G. Tính GA,GB,GC
GIÚP MK VỚI
BC = \(\sqrt{8^2+6^2}\)= 10 cm
trung truyến AM = BC/2 = 5cm
AG = 2AM/3 = 10/3 cm.
trung tuyến BN = \(\sqrt{\frac{2BC^2+2BA^2-AC^2}{4}}\)= \(\sqrt{\frac{2\left(10^2+6^2\right)-8^2}{4}}\)
BG = 2BN/3
trung tuyến CP = \(\sqrt{\frac{2BC^2+2AC^2-AB^2}{4}}\)= \(\sqrt{\frac{2\left(10^2+8^2\right)-6^2}{4}}\)
BG = 2CP/3
Đúng 0
Bình luận (0)
Cho 🔺ABC,G là trọng tâm 🔺.Phân tích véc-tơ AB theo 2 véc-tơ GB và véc-tơ GC
Mn giúp mk vs nạ
\(\overrightarrow{GA}=-\overrightarrow{GB}-\overrightarrow{GC}\)
\(\overrightarrow{AB}=\overrightarrow{GB}-\overrightarrow{GA}=\overrightarrow{GB}+\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GB}+\overrightarrow{GC}\)
Cho tam giác đều ABC cạnh a, đường cao AH, trọng tâm G. Tính:
a, |AC|, |AB + AH|, |AB - AH|
b, |GB|, |GA + GB|, |GA + GB + GC|
Cho tam giác ABC có AB = AC =5cm; BC =8cm. Gọi G là trọng tâm cụa tam giác .Tính GA, GB, GC
Gọi `AM` là trung tuyến của `ΔABC`
`=>AM` đồng thời là đường cao
`=>ΔAMB;ΔAMC⊥M`
`AM` là trung tuyến nên
`BM=MC=(BC)/2=4(cm)`
Áp dụng định lý py-ta-go ta tính được
`AM^2=AB^2-BM^2=5^2-4^2=25-16=9(cm)`
`=>AM=3cm`
`G` trọng tâm
`=>GA=2/3AM=2cm`
`GM=1/3AM=1cm`
Áp dụng định lý py-ta-go lần nữa ta tính đc
`GC^2=BG^2=BM^2+GM^2=4^2+1^2=16+1=17cm`
`=>GB=GC=`\(\sqrt{17cm}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=5cm;BC=13cm. Gọi G là trọng tâm của tam giác ABC.Tính GA+GB+GC
Cho tam giác ABC có AB = AC =5cm; BC =8cm. Gọi G là trọng tâm cụa tam giác .Tính GA, GB, GC

