cho hàm số f(x)=ax^2+bx+c
chứng tỏ rằng f(-2);f(3) nhỏ hơn hoặc băng 0 biết 13a+b+2c=0
Cho \(f\left(x\right)=ax^2+bx+c\) với a,b,c là số hữu tỉ. Chứng tỏ rằng : f(-2) . (f3)\(\le0\)Biết 13a+b+2c=0
\(f\left(x\right)=ax^2+bx+c\)
Ta có : \(f\left(-2\right)=4a-2b+c\)
\(f\left(3\right)=9a+3b+c\)
\(\Rightarrow\) \(f\left(-2\right)+f\left(3\right)=4a-2b+c+9a+3b+c\)
\(=13a+b+c\)
\(=0\)
\(\Rightarrow\) \(-f\left(-2\right)=f\left(3\right)\)
\(\Rightarrow\) \(f\left(-2\right).f\left(3\right)=f\left(-2\right).-f\left(-2\right)=-\left[f\left(-4\right)\right]^2\le0\)
\(\Rightarrow\) \(đpcm\)
Study well ! >_<
f(-2)=\(4a-2b+c\)(1)
f(3)=\(9a+3b+c\)(2)
Lấy (1)+(2) ta được f(-2)+f(3)=13a+b+2c=0
Vì f(-2) và f(3) trái dấu
Suy ra f(-2)=-f(3)
Suy ra f(-2).f(3)=-f(3).f(3)=\(-\left(f^2\left(c\right)\right)\)\(\le\)0(đpcm)
a) Cho đa thức f(x)= ax2+bx+c với a,b,c là các số thực. Biết rằng f(0) ; f(1) ; f(2) có trị nguyên. Chứng minh rằng 2a,2b,2c có giá trị nguyên.
c) Tìm x,y thuộc N biết : 36-y2=8.(x-2010)2
\(f\left(x\right)=ax^2+bx+c\Rightarrow\hept{\begin{cases}f\left(0\right)=c\\f\left(1\right)=a+b+c\\f\left(2\right)=4a+2b+c\end{cases}}\)
\(f\left(0\right)\) nguyên \(\Rightarrow c\) nguyên \(\Rightarrow\hept{\begin{cases}2a+2b\\4a+2b\end{cases}}\) nguyên
\(\Rightarrow\left(4a+2b\right)-\left(2a+2b\right)=2a\)(nguyên)
\(\Rightarrow2b\) nguyên
\(\Rightarrowđpcm\)
\(36-y^2\le36\)
\(8\left(x-2010\right)^2\ge0;8\left(x-2010\right)^2⋮8\)
\(\Rightarrow\hept{\begin{cases}0\le8\left(x-2010\right)^2\le36\\8\left(x-2010\right)^2⋮8\\8\left(x-2010\right)^2\in N\end{cases}}\)
Giai tiep nhe
cho đa thức f(x)= ax^2+bx+c. chứng minh rằng nếu x=1 và x= -1 là nghiệm của đa thức f(x) thì a và c là hai số đối nhau
Cho hàm số y = f(x) được xác định bởi công thức f(x) = 5x2 - 2
a) tính f(-0,5); f(-0,2); f(0,4); f(1); f(25)
b tìm x để f(x) = -2; f(x) = 3
c chứng tỏ rằng với mọi x ∈ R thì f(x) = f(-x)
Hàm số \(f\left(x\right)=5x^2-2\)
a) => \(f\left(-0,5\right)=5.\left(-0,5\right)^2-2\)
\(f\left(-0,5\right)=1,25-2\)
\(f\left(-0,5\right)=-0,75.\)
=> \(f\left(-0,2\right)=5.\left(-0,2\right)^2-2\)
\(f\left(-0,2\right)=0,2-2\)
\(f\left(-0,2\right)=-1,8.\)
=> \(f\left(0,4\right)=5.\left(0,4\right)^2-2\)
\(f\left(0,4\right)=0,8-2\)
\(f\left(0,4\right)=-1,2.\)
=> \(f\left(1\right)=5.1^2-2\)
\(f\left(1\right)=5-2\)
\(f\left(1\right)=3.\)
=> \(f\left(25\right)=5.25^2-2\)
\(f\left(25\right)=3125-2\)
\(f\left(25\right)=3123.\)
Mình chỉ làm câu a) thôi nhé.
Chúc bạn học tốt!
cho hàm số y=f(x)=ax.
a)Biết a=2 tính f(1);f(-2);f(-4).
b)Tìm a biết f(2)=4; vẽ đồ thị hàm số khi a =2;a=–3.
c) Trong các điểm sau điểm nào thuộc đồ thị của hàm số khi a = 2. A ( 1; 4) B (–1; –2) C (–2; 4) D (–2; –4)
a) a = 2
+ y = f(1) = 2.1 = 2
+ y = f(-2) = 2.(-2) = -4
+ y = f(-4) = 2.(-4) = -8
b) f(2) = 4
=> 4 = a.2
=> a = 2
( Vẽ đồ thị hàm số thì bạn tự vẽ được mà :)) Ở đây vẽ hơi khó )
c) Khi a = 2
=> Ta có đồ thị hàm số y = 2x
+ A(1;4)
=> xA = 1 ; yA = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2.1 ( vô lí )
=> A không thuộc đồ thị hàm số y = 2x
+ B = ( -1; -2 )
=> xB = -1 ; yB = -2
Thế vào đồ thị hàm số y = 2x ta có :
-2 = 2(-1) ( đúng )
=> B thuộc đồ thị hàm số y = 2x
+ C(-2; 4)
=> xC = -2 ; yC = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2(-2) ( vô lí )
=> C không thuộc đồ thị hàm số y = 2x
+ D(-2 ; -4 )
=> xD = -2 ; yD = -4
Thế vào đồ thị hàm số y = 2x ta có :
-4 = 2(-2) ( đúng )
=> D thuộc đồ thị hàm số y = 2x
Cho f(x)= ax3+bx2+cx+d. Chứng minh rằng f(x) nhận được giá trị nguyên với mọi x thuộc Z khi và chỉ khi 6a;2b;a+b+c và d là số nguyên.
Cho đa thức \(f\left(x\right)=\)ax^2+bx+c với a, b, c là cá số thực
Biết rằng \(f\left(0\right);f\left(1\right);f\left(2\right)ćo\)giá trị nguyên
cho hai đa thức f(x)=(ax^2+bx+c) với a,b,c là các số hữu tỉ thỏa mãn 2a-b=0. chứng minh rằng f(-5).(f(3) ko thể là số âm
giúp mk với các bn mk đg cần gấp!!!!!
ai nhanh mk tik cho!
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng y=f(x) là một trong bốn hàm được đưa ra trong các phương án dưới đây. Tìm y=f(x)
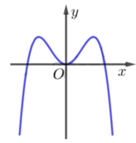
A. f x = − x 4 + 2 x 2
B. f x = − x 4 + 2 x 2 − 1
C. f x = x 4 + 2 x 2
D. f x = x 4 − 2 x 2