Cho tam giác ABC, đường cao AH. Gọi M;N là trung điểm của các cạnh AB và AC. Chứng minh:
a) MN là phân giác góc AMH
b) AHM + ABH = 90
( kiến thức lớp 7 )
Giúp mình với mình cần gấp.
Giúp tớ với
1. Cho tam giác ABC có đường cao AH. Gọi M, N là hình chiếu của H trên AB, AC. Chứng minh: tam giác ABC đồng dạng với tam giác ANM
2.Cho tam gíac ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC, biết AH= 12cm , BH= 9cm .
3.Cho tam giác ABC, biết BC =7,5cm , CA =4,5 cm , AB= 6 cm . a) Tam giác ABC là tam giác gì ? Tính đường cao AH của tam giác ABC; b) Tính độ dài các đoạn BH, CH
4.. Cho hình bình hành ABCD có góc A nhọn. Gọi I, K lần lượt là hình chiếu của B, D trên đường chéo AC. Gọi M và N lần lượt là các hình chiếu của C trên đường thẳng AB, AD. Chứng minh:
a) AK= IC .
b) Tứ giác BIDK là hình bình hành.
c) 2 AC AD AN AB AM
Cho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEH. AB>AC
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
Cho tam giác ABC, đường cao AH,(H thuộc BC). Vẽ ra phía ngoài tam giác ABC của tam giác vuông cân ở A là tam giác ABD và tam giác ACE .Gọi điểm M là giao điểm của đường thưởng AH và BE. Gọi i là hình chiếu vuông góc của điểm D lên AH . Chứng minh rằng
a. Góc HDA= góc BAH
b.tam giác AHD=tam giác BHA
c. MD=ME
sos giúp e với ạ :(
Cho tam giác ABC vuông tại A , đường cao AH. Gọi M là trung điểm BC . Biết AH =2, AC =4 .Tính chu vi tam giác MAC
Lời giải:
Áp dụng định lý Pitago:
$HC=\sqrt{AC^2-AH^2}=\sqrt{4^2-2^2}=2\sqrt{3}$
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{2^2}{2\sqrt{3}}=\frac{2\sqrt{3}}{3}$
$BC=BH+CH=\frac{2\sqrt{3}}{3}+2\sqrt{3}=\frac{8\sqrt{3}}{3}$
$\Rightarrow MC=BC:2=\frac{4\sqrt{3}}{3}$
$AM$ là trung tuyến ứng với cạnh huyền nên $AM=\frac{BC}{2}=\frac{4\sqrt{3}}{3}$
Chu vi $MAC$:
$MA+MC+AC=\frac{4\sqrt{3}}{3}+\frac{4\sqrt{3}}{3}+4=\frac{12+8\sqrt{3}}{3}$
Cho tam giác ABC có đường cao AH = 6cm, diện tích tam giác ABC là 30 c m 2 . Gọi M là trung điểm của BC. Tính diện tích tam giác ABM
A. 10 c m 2
B. 12 c m 2
C. 20 c m 2
D. 15 c m 2
Cho tam giác ABC nhọn gọi AH,BI,CK là 3 đường cao. C/m tam giác AIK đồng dạng tam giác ABC
Ban đầu xét tam giác AIB và tam giác AKC có :
góc BAC chung ; góc AKC= góc AIB =90 độ (g)
Do vậy tam giác AIB đồng dạng tam giác AKC (g-g)
=> AI/AB=AK/AC (1)
Xét tam giác AIK và tam giác ABC có :
góc BAC chung ; AI/AB=AK/AC (theo (1))
Do vậy tam giác AIK đồng dạng tam giác ABC (c-g-c)
xét tam giác AIB và tam giác AKC có :
góc BAC chung ; góc AKC= góc AIB =90 độ (g)
Do vậy tam giác AIB đồng dạng tam giác AKC (g-g)
=> AI/AB=AK/AC (1)
Xét tam giác AIK và tam giác ABC có :
góc BAC chung ; AI/AB=AK/AC (theo (1))
Do vậy tam giác AIK đồng dạng tam giác ABC (c-g-c)
cho tam giác ABC đường cao AH. Gọi M là trung điểm của BC, biết AH, AM chia góc ở đỉnh A thành 3 góc bằng nhau. Tính các của tam giác ABC.
Cho tam giác ABC cân tại A. Vẽ đường cao AH
a) CM:tam giác ABH=tam giác ACH
b) Gọi G là điểm thuộc AH sa cho GH=1phần 3 AH. CM:G là trọng tâm của tam giác ABC
c) CM: tam giác BGC cân
d) gọi M là trung điểm AC. CM: B,G,M thẳng hàng
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
Chứng minh rằng S ' S = D K A H
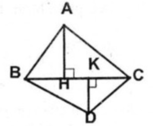
Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'
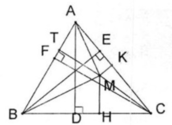
Cho tam giác ABC ; đường cao AH . Gọi M là trung điểm của BC . Biết AH, AM chia góc ở đỉnh A thành ba góc bằng nhau . Tính các góc của tam giác ABC