Cho tam giác ABC có G là trọng tâm, lấyP trên BC các đường thẳng đi qua P và song song với CG;BG cắt AB;AC ở E;F đường thẳng EF cắt BG;CG lần lượt tại I và K. CMR
a) EI=IK=KF
b) PQ đi qua trung điểm của EF
H24
Những câu hỏi liên quan
Cho tam giác ABC có G là trọng tâm, lấyP trên BC các đường thẳng đi qua P và song song với CG;BG cắt AB;AC ở E;F đường thẳng EF cắt BG;CG lần lượt tại I và K. CMR
a) EI=IK=KF
b) PQ đi qua trung điểm của EF
cho tam giác ABC có trọng tâm G. 1 điểm K thuộc BC. Các đường thẳng đi qua K theo thứ tự song song với CG và BG cắt AC lần Lượt tại E;F. Gọi giao của EF với BG và CG là I;J. Chứng minh EI=IJ=JF.
b.Chứng minh KG đi qua trung điểm BF.
Cho tam giác ABC trọng tâm G. Một điểm bất kì thuộc canh BC. Qua P kẻ các đường thẳng song song với CG, BG cắt AB và AC ở E và F, EF cắt BG, CG ở I và K. Chứng minh:
a) EI = IK = KF
b) PG đi qua trung điểm của EF
Cho tam giác ABC có đường cao AH trọng tâm G. Một đường thẳng đi qua G và song song với BC cắt các cạnh AB, AC tại M và N. Nếu diện tích tam giác ABC bằng 36 cm2 thì diện tích tam giác HMN bằng ... cm2
cho tam giác ABC có đường cao AH trọng tâm G một đường thẳng đi qua G và song song với BC . Cắt các cạnh AB, AC tại M và N .Nếu diện tích tam giác ABC bằng 36 cm2 thì diện tích tam giác HMN bằng
Cho tam giác ABC có đường cao AH trọng tâm G. Một đường thẳng đi qua G
và song song với BC cắt các cạnh AB, AC tại M và N. Nếu diện tích tam giác ABC bằng 36
thì diện tích tam giác HMN bằng
Ta có: MN II BC => HK\(⊥\)MN
Theo Talet có: \(\frac{HK}{AH}=\frac{GD}{AD}=\frac{1}{3}\)
và: \(\frac{MG}{BD}=\frac{AG}{AD}=\frac{2}{3}\)(*)
\(\frac{GN}{DC}=\frac{AG}{AD}=\frac{2}{3}\)(**)
tỪ (*) và (**) => \(\frac{MN}{BC}=\frac{2}{3}\)
Vậy diện tích tam giác HMN=\(S_{HMN}=\frac{2}{9}.S_{ABC}=\frac{2.36}{9}=8\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SASBCACBABa,
S
C
a
3
2
, G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng A. ...
Đọc tiếp
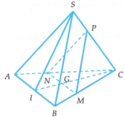
Cho hình chóp S.ABC có SA=SB=CA=CB=AB=a, S C = a 3 2 , G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng
A. 90 0 C
B. 45 0 C
C. 30 0 C
D. 60 0 C
Chọn đáp án D
Ta có
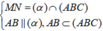
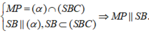
Khi đó 
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
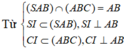
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi G là trọng tâm của tam giác. Qua G kẻ đường thẳng song song với AB nó cắt BC tại D, kẻ đường thẳng song song với AC, nó cắt BC tại E. a. So sánh các tỉ số BD/BC và EC/BC b. Chứng minh BD = DE = EC
gfvfvfvfvfvfvfv555
Cho tam giác ABC có đường cao AH, trọng tâm G. Kẻ đường thẳng đi qua G và song song với BC cắt các cạnh AB, AC tại M, N. Nếu diện tích tam giác ABC bằng 36 \(cm^2\)thì diện tích tam giác HMN=?