tam giác ABC phân giác AD, trung tuyến AM đường tròn (O) đi qua ADM giao AB;AC ở E,F
a,so sánh BE và CF
b, A=90 độ cm: căn (2)/AD=1/AB + 1/AC
TH
Những câu hỏi liên quan
cho tam giác abc vẽ đường trung tuyến am đường phân giác ad đường tròn ngoại tiếp tam giác adm cắt ab, ac theo thứ tự ở e và f. cmr be=cf
Cho tam giác ABC, đường trung tuyến AM, đường phân giác AD. Đường tròn ngoại tiếp tam giác ADM cắt AB, AC theo thứ tự ở E, F. Chứng minh rằng BE = CF.
LÀM ƠN GIÚP VỚI! 1, tam giác ABC phân giác AD, trung tuyến AM đường tròn (O) đi qua ADM giao AB;AC ở E,Fa,so sánh BE và CFb, A90 độ cm: căn (2)/AD1/AB + 1/AC2,cho góc xOy trên Ox lấy AB ;Oy lấy CD sao cho ABCD. M,N là trung điểm của AC; BDcmr MN // phân giác xOy3, tam giác ABC cân tại A. đường cao AH, HE vuông góc AC, AI vuông góc BE (I thuộc BE); AI căt HE tại Mcm: MHME
Đọc tiếp
LÀM ƠN GIÚP VỚI!
1, tam giác ABC phân giác AD, trung tuyến AM đường tròn (O) đi qua ADM giao AB;AC ở E,F
a,so sánh BE và CF
b, A=90 độ cm: căn (2)/AD=1/AB + 1/AC
2,cho góc xOy trên Ox lấy AB ;Oy lấy CD sao cho AB=CD. M,N là trung điểm của AC; BD
cmr MN // phân giác xOy
3, tam giác ABC cân tại A. đường cao AH, HE vuông góc AC, AI vuông góc BE (I thuộc BE); AI căt HE tại M
cm: MH=ME
Bài 7: (3 điểm) Cho tam giác ABC (AC AB) trung tuyến AM, lấy điểm N thuộc AM (điểm N nằm giữa A và M) vẽ đường tròn (O) đường kính AN. a) Gọi F là giao điểm của phân giác trong AD với (O). gọi E là giao điểm của phân giác ngoài góc A với (O). Chứng minh EF là đường kính của đường tròn (O)b) Đường tròn (O) cắt AB ở K, cắt AC ở H. KH cắt AD ở I. Chứng minh: FK. FK FIFAc) CMR : NH.CD NK. BD (mấy bạn sửa dùm tui câu c he )
Đọc tiếp
Bài 7: (3 điểm) Cho tam giác ABC (AC > AB) trung tuyến AM, lấy điểm N thuộc AM (điểm N nằm giữa A và M) vẽ đường tròn (O) đường kính AN.
a) Gọi F là giao điểm của phân giác trong AD với (O). gọi E là giao điểm của phân giác ngoài góc A với (O). Chứng minh EF là đường kính của đường tròn (O)
b) Đường tròn (O) cắt AB ở K, cắt AC ở H. KH cắt AD ở I. Chứng minh: FK. FK = FIFA
c) CMR : NH.CD = NK. BD (mấy bạn sửa dùm tui câu c he )
Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD . T ính diện tích tam giác ADM,biết AB = m, AC = n (n > m) và diện tích của tam giác ABC là S.
Cho tam giác ABC nhọn (ABAC), kẻ phân giác AD của góc BAC và đường trung tuyến AM (M,D thuộc BC). Vẽ 2 đường tròn ngoại tiếp các tam giác ABC và ADM, 2 đường tròn này cắt nhau tại điểm thứ 2 là I, đường tròn ngoại tiếp tam giác ADM cắt 2 cạnh AB và AC theo thứ tự tại E và F. Tia AD cắt đường tròn ngoại tiếp tam giác ABC tại J.a, Chứng minh 3 điểm I; M; J thẳng hàng.b, Gọi K là trung điểm È, tia MK cắt AC và tia BA theo thứ tự tại P và Q. Chứng minh tam giác PAQ cân
Đọc tiếp
Cho tam giác ABC nhọn (AB<AC), kẻ phân giác AD của góc BAC và đường trung tuyến AM (M,D thuộc BC). Vẽ 2 đường tròn ngoại tiếp các tam giác ABC và ADM, 2 đường tròn này cắt nhau tại điểm thứ 2 là I, đường tròn ngoại tiếp tam giác ADM cắt 2 cạnh AB và AC theo thứ tự tại E và F. Tia AD cắt đường tròn ngoại tiếp tam giác ABC tại J.
a, Chứng minh 3 điểm I; M; J thẳng hàng.
b, Gọi K là trung điểm È, tia MK cắt AC và tia BA theo thứ tự tại P và Q. Chứng minh tam giác PAQ cân
a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác trong AD. Tính diện tích tam giác ADM, biết AB = m, AC = n (n > m) và diện tích tam giác ABC là S.
b) Khi cho n = 7cm, m = 3cm, hỏi rằng diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC?
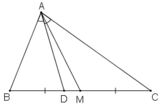
a) Ta có: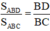 
(do hai tam giác có chung chiều cao từ đỉnh A)
ΔABC có AD là phân giác
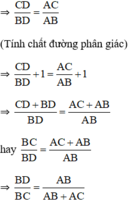
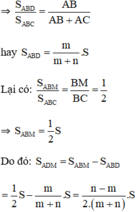
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:
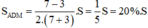
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5 cm. Kẻ các đường phân giác AD, trung tuyến AM (M, D thuộc cạnh BC). Tính diện tích tam giác ADM.
Kẻ \(AH\perp BC\left(H\in BC\right)\)
Ta có: \(AB^2+AC^2=BC^2\left(3^2+4^2=5^2\right)\Rightarrow\Delta ABC\) vuông tại A
\(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH.5=3.4\Rightarrow AH=2,4\left(cm\right)\)
AD là tia p/g của \(\widehat{BAC}\left(D\in BC\right)\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}=\frac{3}{4}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{3}{3+4}\Rightarrow\frac{DB}{BC}=\frac{3}{7}\Rightarrow\frac{DB}{5}=\frac{3}{7}\Rightarrow DB=\frac{15}{7}\left(cm\right)\)
\(BM=\frac{1}{2}BC=\frac{1}{2}.5=\frac{5}{2}\left(cm\right)\)
Do đó: \(DM=BM-BD=\frac{5}{2}-\frac{15}{7}=\frac{5}{14}\left(cm\right)\)
Vậy \(S_{ADM}=\frac{1}{2}AH.DM=\frac{1}{2}.2,4.\frac{5}{14}=\frac{3}{7}\left(cm^2\right)\)
Đúng 0
Bình luận (0)
a) cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM biết AB=m, AC =n (n>m)và diện tích của tam giác ABC là S
b)cho n=7 cm, m=3cm ,hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC